(本小题满分15分)已知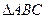 的面积
的面积 满足
满足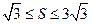 ,且
,且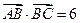 .
.
(1)求角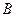 的取值范围;(2)求函数
的取值范围;(2)求函数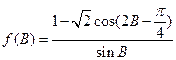 的值域.
的值域.
(本小题满分14分)已知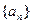 的首项为a1,公比q为正数(q≠1)的等比数列,其前n项和为Sn,且
的首项为a1,公比q为正数(q≠1)的等比数列,其前n项和为Sn,且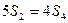 .(1)求q的值;(2)设
.(1)求q的值;(2)设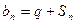 ,请判断数列
,请判断数列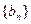 能否为等比数列,若能,请求出a1的值,否则请说明理由.
能否为等比数列,若能,请求出a1的值,否则请说明理由.
(本小题满分14分)已知全集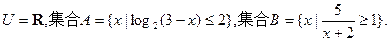
(1)求A、B;(2)求
(本小题满分14分)已知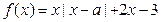 (Ⅰ)当
(Ⅰ)当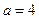 ,
,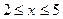 时,问
时,问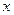 分别取何值时,函数
分别取何值时,函数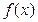 取得最大值和最小值,并求出相应的最大值和最小值;(Ⅱ)若
取得最大值和最小值,并求出相应的最大值和最小值;(Ⅱ)若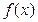 在R上恒为增函数,试求
在R上恒为增函数,试求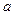 的取值范围;
的取值范围;
(Ⅲ)已知常数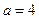 ,数列
,数列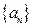 满足
满足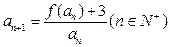 ,试探求
,试探求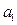 的值,使得数列
的值,使得数列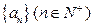 成等差数列.
成等差数列.
(本小题满分12分)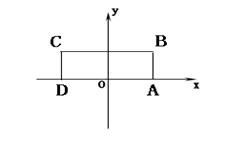
如图,在矩形ABCD中,已知A(2,0)、C(-2,2),点P在BC边上移动,线段OP的垂直平分线交y轴于点E,点M满足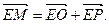 (Ⅰ)求点M的轨迹方程;
(Ⅰ)求点M的轨迹方程;
(Ⅱ)已知点F(0,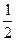 ),过点F的直线l与点M的轨迹相交于Q、R两点,且
),过点F的直线l与点M的轨迹相交于Q、R两点,且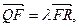 求实数
求实数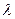 的取值范围.
的取值范围.