如图:EF∥AD ,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整:
因为EF∥AD,所以∠2=__
又因为∠1=∠ 2,所以∠1=∠3
2,所以∠1=∠3
所以AB∥__
所以∠BAC+__=180°
因为∠BAC=70°,所以∠AGD=__
已知方程组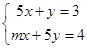 与
与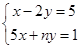 有相同的解,求m2-2mn+n2的值
有相同的解,求m2-2mn+n2的值
化简(本题6分)
(1)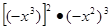
(2)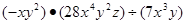
已知:如图1,矩形ABCD中,AB=6,BC=8,E、F、G、H分别是AB、BC、CD、DA四条边上的点(且不与各边顶点重合),设m=EF+FG+GH+HE,探索m的取值范围.
(1)如图2,当E、F、G、H分别是AB、BC、CD、DA四边中点时,m=.
(2)为了解决这个问题,小贝同学采用轴对称的方法,如图3,将整个图形以CD为对称轴
翻折,接着再连续翻折两次,从而找到解决问题的途径,求得m的取值范围.①请在图3
中补全小贝同学翻折后的图形;②请你根据①中的图形,求出m的取值范围,并简要说明理
由.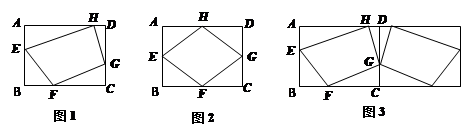
如图,以OA1=2为底边做等腰三角形,使得第三个顶点C1恰好在直线y=x+2上,并以此向左、右依次类推,作一系列底边为2,第三个顶点在直线y=x+2上的等腰三角形.
(1)请你通过计算说明:底边为2,顶点在直线y=x+2上且面积为21的等腰三角形位于图
中什么位置?
(2)求证:y轴右侧的每一个等腰三角形的面积都等于前后两个以腰为一边的三角形面积之和的一半(如:S右1=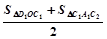 ,S右2=
,S右2=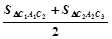 ).
).
(3)过D1、A1、C2三点画抛物线.问在抛物线上是否存在点P,使得△PD1C2的面积是△C1OD1与△C1A1C2面积和的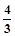 .若存在,请求出点P的坐标;若不存在,请说明理由.
.若存在,请求出点P的坐标;若不存在,请说明理由.
如图,菱形ABCD的边长为30 cm,∠A=120°.点P沿折线A-B-C-D运动,速度为1 cm/s;点Q沿折线A-D-C- B运动,速度为 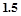 cm/s.当一点到达终点时,另一点也随即停止运动.若点P、Q同时从点A出发,运动时间为t s.
cm/s.当一点到达终点时,另一点也随即停止运动.若点P、Q同时从点A出发,运动时间为t s.
(1)设△APQ面积为s cm2,求s与t的函数关系式,并写出自变量t的取值范围;
(2)当△APQ为等腰三角形时,直接写出t的值.