已知:如图1,矩形ABCD中,AB=6,BC=8,E、F、G、H分别是AB、BC、CD、DA四条边上的点(且不与各边顶点重合),设m=EF+FG+GH+HE,探索m的取值范围.
(1)如图2,当E、F、G、H分别是AB、BC、CD、DA四边中点时,m= .
(2)为了解决这个问题,小贝同学采用轴对称的方法,如图3,将整个图形以CD为对称轴
翻折,接着再连续翻折两次,从而找到解决问题的途径,求得m的取值范围.①请在图3
中补全小贝同学翻折后的图形;②请你根据①中的图形,求出m的取值范围,并简要说明理
由.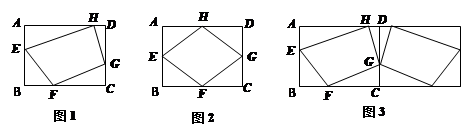
将抛物线 向下平移6个单位长度得到抛物线 ,再将抛物线 向左平移2个单位长度得到抛物线 .
(1)直接写出抛物线 , 的解析式;
(2)如图(1),点 在抛物线 (对称轴 右侧)上,点 在对称轴 上, 是以 为斜边的等腰直角三角形,求点 的坐标;
(3)如图(2),直线 , 为常数)与抛物线 交于 , 两点, 为线段 的中点;直线 与抛物线 交于 , 两点, 为线段 的中点.求证:直线 经过一个定点.

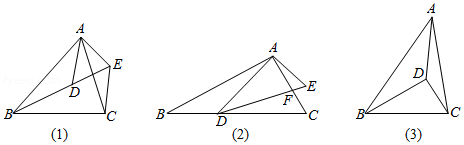
问题背景 如图(1),已知 ,求证: ;
尝试应用 如图(2),在 和 中, , , 与 相交于点 ,点 在 边上, ,求 的值;
拓展创新 如图(3), 是 内一点, , , , ,直接写出 的长.
某公司分别在 , 两城生产同种产品,共100件. 城生产产品的总成本 (万元)与产品数量 (件 之间具有函数关系 .当 时, ;当 时, . 城生产产品的每件成本为70万元.
(1)求 , 的值;
(2)当 , 两城生产这批产品的总成本的和最少时,求 , 两城各生产多少件?
(3)从 城把该产品运往 , 两地的费用分别为 万元 件和3万元 件;从 城把该产品运往 , 两地的费用分别为1万元 件和2万元 件. 地需要90件, 地需要10件,在(2)的条件下,直接写出 , 两城总运费的和的最小值(用含有 的式子表示).
如图,在 中, ,以 为直径的 交 于点 , 与过点 的切线互相垂直,垂足为 .
(1)求证: 平分 ;
(2)若 ,求 的值.

在 的网格中建立如图的平面直角坐标系,四边形 的顶点坐标分别为 , , , .仅用无刻度的直尺在给定网格中按下列步骤完成画图,并回答问题:
(1)将线段 绕点 逆时针旋转 ,画出对应线段 ;
(2)在线段 上画点 ,使 (保留画图过程的痕迹);
(3)连接 ,画点 关于直线 的对称点 ,并简要说明画法.
