如图,已知点P是三角形ABC外一点,且 底面
底面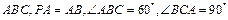 ,点
,点 ,
, 分别在棱
分别在棱 上,且
上,且 。 。
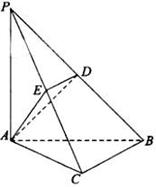
。 。 
(1)求证: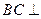 平面
平面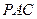 ;
;
(2)当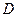 为
为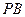 的中点时,求
的中点时,求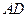 与平面
与平面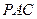 所成的角的大小;
所成的角的大小;
(3)是否存在点 使得二面角
使得二面角 为直二面角?并说明理由.
为直二面角?并说明理由.
(本小题13分)某食品厂定期购买面粉,已知该厂每天需要面粉6吨,每吨面粉价格为1800元,面粉的保管费为平均每天每6吨18元(从面粉进厂起开始收保管费,不足6 吨按6 吨算),购面粉每次需要支付运费900元,设该厂每 天购买一次面粉。(注:该厂每次购买的面粉都能保证使用整数天)
天购买一次面粉。(注:该厂每次购买的面粉都能保证使用整数天)
(Ⅰ)计算每次所购买的面粉需支付的保管费是多少?
(Ⅱ)试求 值,使平均每天所支付总费用最少?并计算每天最少费用是多少?
值,使平均每天所支付总费用最少?并计算每天最少费用是多少?
(本小题12分)已知B(-2,0),C(2,0)是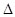 ABC的两个顶点,且满足
ABC的两个顶点,且满足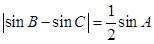 ,
,
(Ⅰ)求顶点A的轨迹方程
(Ⅱ)过点C作倾斜角为 的直线交点A的轨迹于E、F两点,求|EF|
的直线交点A的轨迹于E、F两点,求|EF|
(本小题12分)点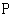 在椭圆
在椭圆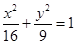 上,求点
上,求点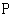 到直线
到直线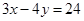 的最大距离和最小距离。
的最大距离和最小距离。
(本小题12分)等差数列 中,
中,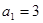 ,其前
,其前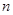 项和为
项和为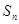 .等比数列
.等比数列 的各项均为正数,
的各项均为正数,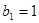 ,且
,且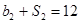 ,
,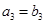 .
.
(Ⅰ)求数列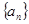 与
与 的通项公式;(Ⅱ)求数列
的通项公式;(Ⅱ)求数列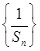 的前
的前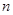 项和
项和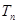 .
.
(本小题12分)设命题 实数
实数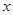 满足
满足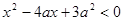 ,其中
,其中 ,命题
,命题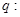 实数
实数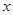 满足
满足 .
.
(Ⅰ)若 ,且
,且 为真,求实数
为真,求实数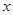 的取值范围;
的取值范围;
(Ⅱ)若 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数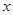 的取值范围.
的取值范围.