已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =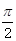 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .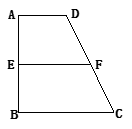
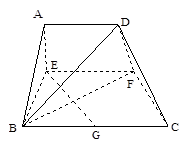
(1) 当x=2时,求证:BD⊥EG ;
(2) 若以F、B、C、D为顶点的三棱锥的体积记为f(x),求f(x)的最大值;
(3) 当f(x)取得最大值时,求二面角D-BF-C的余弦值.
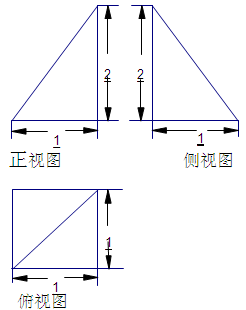
已知四棱锥 的三视图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形. 是侧棱
是侧棱 上的动点.
上的动点.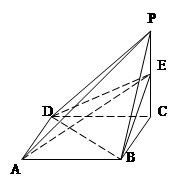
(1)求证: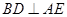 ;
;
(2)若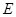 为
为 的中点,求直线
的中点,求直线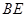 与平面
与平面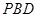 所成角的正弦值;
所成角的正弦值;
(3) 若四点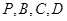 在同一球面上,求该球的体积.
在同一球面上,求该球的体积.
如图,在直三棱柱ABC—A1B1C1中, 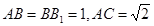 ,直线B1C与平面ABC成45°角.
,直线B1C与平面ABC成45°角.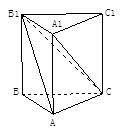
(1)求证:平面A1B1C⊥平面B1BCC1;
(2)求二面角A—B1C—B的余弦值.
在空间直角坐标系中,已知O (0,0,0) ,A(2,-1,3),B(2,1,1).
(1)求|AB|的长度;
(2)写出A、B两点经此程序框图执行运算后的对应点A0,B0的坐标,并求出 在
在 方向上的投影.
方向上的投影.
在长方体 中,
中,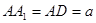 ,
,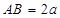 ,
,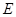 、
、  分别为
分别为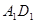 、
、 的中点.
的中点.
(1)求证: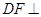 平面
平面 ;
;
(2)求证: 平面
平面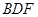 .
.