(本小题满分13分)
如图PA⊥平面ABCD,四边形ABCD是矩形,E、F分别是AB,PD的中点.
(1)求证:AF//平面PCE;
(2)若PA=AD且AD=2,CD=3,求P—CE—A的正切值.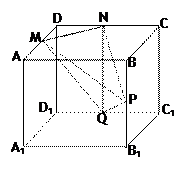
已知等比数列 单调递增,
单调递增,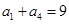 ,
, ,
, .
.
(Ⅰ)求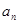 ;
;
(Ⅱ)若 ,求
,求 的最小值.
的最小值.
已知函数 .
.
(1)当 时,求
时,求 在
在 最小值;
最小值;
(2)若 存在单调递减区间,求
存在单调递减区间,求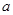 的取值范围;
的取值范围;
(3)求证: (
(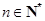 ).
).
已知函数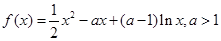 ,
,
(1)讨论函数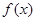 的单调性;
的单调性;
(2)证明:若 ,则对于任意
,则对于任意 有
有 。
。
某厂家拟在2013年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量) 万件与年促销费用
万件与年促销费用 万元满足
万元满足 (
( 为常数),如果不搞促销活动,则该产品的年销售量是1万件. 已知2013年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的
为常数),如果不搞促销活动,则该产品的年销售量是1万件. 已知2013年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的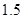 倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
(1)将2013年该产品的利润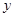 万元表示为年促销费用
万元表示为年促销费用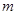 万元的函数;
万元的函数;
(2)该厂家2013年的促销费用投入多少万元时,厂家的利润最大?
已知函数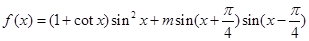 ,
,
(1)当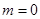 时,求
时,求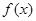 在区间
在区间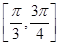 上的取值范围;
上的取值范围;
(2)当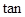
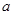 =2时,
=2时,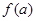 =
= ,求
,求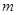 的值。
的值。