(本小题满分12分)
椭圆C的中心为坐标原点O,焦点在y轴上,短轴长为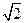 、离心率为
、离心率为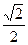 ,直线
,直线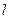 与y轴交于点P(0,
与y轴交于点P(0,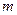 ),与
),与 椭圆C交于相异两点A、B,且
椭圆C交于相异两点A、B,且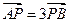 。
。
(I)求椭圆方程;
(II)求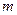 的取值范围。
的取值范围。
已知数列{an}和{bn}满足:a1= ,an+1=
,an+1= an+n-4,bn=(-1)n(an-3n+21),其中
an+n-4,bn=(-1)n(an-3n+21),其中 为实数,n为正整数.
为实数,n为正整数.
(1)证明:对任意实数 ,数列{an}不是等比数列;
,数列{an}不是等比数列;
(2)证明:当 ≠-18时,数列{bn}是等比数列;
≠-18时,数列{bn}是等比数列;
(3)设Sn为数列{bn}的前n项和.是否存在实数 ,使得对任意正整数n,都有Sn>-12?若存在,求
,使得对任意正整数n,都有Sn>-12?若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
已知数列{an}、{bn}满足:a1=2,b1=1,
且 (n≥2).
(n≥2).
(1)令cn=an+bn,求数列{cn}的通项公式;
(2)求数列{an}的通项公式及前n项和公式Sn.
假设某市2008年新建住房400万平方米,其中有250万平方米是中低价房,预计在今后的若干年内,该市每年新建住房面积平均比上一年增长8%.另外,每年新建住房中,中低价房的面积均比上一年增加50万平方米.那么,到哪一年底,
(1)该市历年所建中低价房的累计面积(以2008年为累计的第一年)将首次不少于4 750万平方米?
(2)当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%?(参考数据:1.084≈1.36,1.085≈1.47,
1.086≈1.59)
已知f(x)=logax(a>0且a≠1),设f(a1),f(a2),…,f(an) (n∈N*)是首项为4,公差为2的等差数列.
(1)设a为常数,求证:{an}成等比数列;
(2)若bn=anf(an),{bn}的前n项和是Sn,当a= 时,求Sn.
时,求Sn.
数列{an}的前n项和为Sn,a1=1,an+1=2Sn(n∈N*).
(1)求数列{an}的通项an;
(2)求数列{nan}的前n项和Tn.