(本小题满分12分)
某校高三数学竞赛初赛考试后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,第一组 、第二组
、第二组 …第六组
…第六组 . 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
. 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
(Ⅰ)请补充完整频率分布直方图,并估
计这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第四组和第六组中任意选2人,记他们的成绩分别为 . 若
. 若 ,则称此二人为“黄金帮扶组”,试求选出的二人为“黄金帮扶组”的概率
,则称此二人为“黄金帮扶组”,试求选出的二人为“黄金帮扶组”的概率 ;
;
(Ⅲ)以此样本的频率当作概率,现随机在这组样本中选出的3名学生,求成绩不低于120分的人数 分布列及期望.
分布列及期望.
(本小题满分14分)已知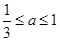 , 若函数
, 若函数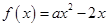 在
在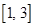 上的最大值为
上的最大值为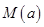 ,最小值为
,最小值为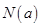 , 令
, 令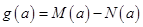 .
.
(1)求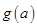 的表达式;
的表达式;
(2)若关于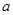 的方程
的方程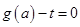 有解,求实数
有解,求实数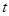 的取值范围.
的取值范围.
(本小题满分14分)已知圆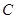 的圆心坐标为
的圆心坐标为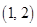 , 直线
, 直线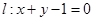 与圆
与圆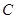 相交于
相交于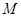 、
、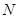 两点,
两点,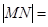
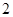 .
.
(1)求圆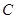 的方程;
的方程;
(2)若 , 过点
, 过点 作圆
作圆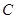 的切线, 切点为
的切线, 切点为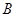 ,记
,记
 , 点
, 点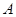 到直线
到直线 的距离为
的距离为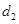 , 求
, 求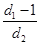 的取值范围.
的取值范围.
(本小题满分14分)已知等差数列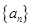 的前
的前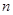 项和为
项和为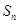 ,且
,且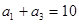 ,
, 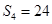 .
.
(1)求数列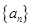 的通项公式;
的通项公式;
(2)令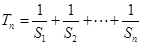 ,求证:
,求证: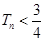 .
.
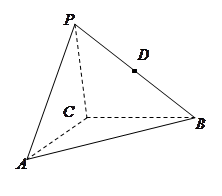
(本小题满分14分)如图,在三棱锥 中,
中, ,点
,点 是线段
是线段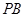 的中点,平面
的中点,平面 平面
平面 .
.
(1)在线段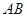 上是否存在点
上是否存在点 , 使得
, 使得 平面
平面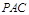 ? 若存在, 指出点
? 若存在, 指出点 的位置, 并加以证明;若不存在, 请说明理由;
的位置, 并加以证明;若不存在, 请说明理由;
(2)求证: .
.
(本小题满分12分)在△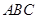 中,角
中,角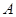 、
、 、
、 所对的边分别为
所对的边分别为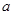 、
、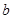 、
、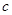 ,已知
,已知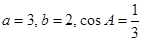 .
.
(1)求 的值;
的值;
(2)求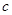 的值.
的值.