(本小题满分12分)
已知函数f(x)=alnx,(a∈R)g(x)=x2,记F(x)=g(x)-f(x)
(Ⅰ)判断F(x)的单调性;
(Ⅱ)当a≥时,若x≥1,求证:g(x-1)≥f();
(Ⅲ)若F(x)的极值为,问是否存在实数k,使方 程g(x)-f(1+x2)=k有四个不同实数根?若存在,求出实数k的取值范围;若不存在,请说明理由。
程g(x)-f(1+x2)=k有四个不同实数根?若存在,求出实数k的取值范围;若不存在,请说明理由。
数列 的各项均为正数,
的各项均为正数,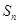 为其前n项和,对于任意的
为其前n项和,对于任意的 ,总有
,总有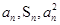 成等差数列
成等差数列
(1)求数列 的通项公式:
的通项公式:
(2)设数列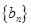 前n项和为
前n项和为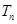 ,且
,且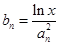 ,求证对任意的实数
,求证对任意的实数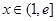 和任意的正整数n,总有
和任意的正整数n,总有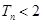 .
.
如图,四棱锥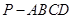 中,
中,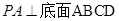 .
. ,F为PC的中点,
,F为PC的中点,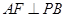 .
.
(1)求 的长:
的长:
(2)求二面角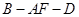 的正弦值.
的正弦值.
盒中共有9个球,其中有4个红球,3个黄球和2个绿球,这些球除颜色外完全相同
(1)从盒中一次随机抽出2个球,求取出的2个球颜色相同的概率:
(2)从盒中一次随机抽出4个球,其中红球,黄球,绿球的个数分别记为 ,随机变量X表示
,随机变量X表示 中的最大数,求X的概率分布列和数学期望
中的最大数,求X的概率分布列和数学期望 .
.
已知锐角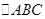 中,角A、B、C所对的边分别为a,b,c,且
中,角A、B、C所对的边分别为a,b,c,且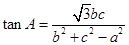
(1)求角A的大小:
(2)求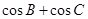 的取值范围.
的取值范围.
已知函数 .
.
(1)若对于 都有
都有 成立,试求a的取值范围;
成立,试求a的取值范围;
(2)记 ,当
,当 时,函数
时,函数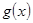 在区间
在区间 上有两个零点,求实数b的取值范围.
上有两个零点,求实数b的取值范围.