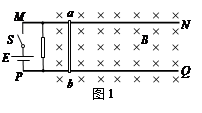火箭是利用反冲原理工作的重要航天运输工具。
（1）我国长征3号甲火箭在起飞阶段，通过发动机喷射气体而获得的反冲力约为火箭总重量的2倍左右。假设在它刚刚起飞后竖直上升的某时刻，火箭的速度大小为v，在此后一个较短的时间t内，发动机喷出的气体质量为△m，喷出的气体相对于地面的速度方向向下，大小为u，求这一段时间内火箭受到的反冲力大小。（计算时忽略喷出气体的重力大小，且认为此段时间内火箭受到的反冲力大小不变）
（2）火箭有单级和多级之分，多级火箭就是把火箭一级一级地接在一起，第一级燃料用完之后把箭体抛弃，减轻负担，然后第二级开始工作，燃料用完之后再把第二级抛弃……，因此从理论上讲，多级火箭能比单级火箭获得更大的速度。
某同学分别建立了以下两个力学模型来粗略地模拟单级火箭和二级火箭在水平飞行时的工作过程，如图甲、乙所示。甲图中的光滑水平面上并排静止放置有质量分别为2m和m的两个物块A、B，它们之间粘有微量的炸药C，爆炸时释放出的能量为2△E；乙图中光滑水平面上并排静止放置有质量均为m的三个物块D、F、G，D、F之间和F、G之间分别粘有微量的炸药P和Q，通过控制使炸药Q先爆炸，炸药P后爆炸，Q和P爆炸时释放出的能量均为△E。所有炸药的质量都忽略不计，爆炸的时间极短，爆炸产生的能量都转化为机械能，爆炸后所有物块的速度方向在同一直线上。求所有的爆炸都发生后物块D的速度是物块A的速度的倍数。
如图所示，匀强磁场沿水平方向，垂直纸面向里，磁感强度B=1T，匀强电场方向水平向右，场强
N/C。一带正电的微粒质量m=2×10-6kg，电荷量q=2×10-6C，在此空间恰好做匀速直线运动，问：
（1）带电微粒运动速度的大小和方向怎样？
（2）若微粒运动到P点时刻，突然将磁场撤去，那么经多少时间微粒到达Q点？（设PQ连线与电场方向平行）
如图所示，在x轴上方有垂直于xy平面向里的匀强磁场，磁感应强度为B；在x轴下方有沿y轴负方向的匀强电场，场强为E。一质量为m，电量为－q的粒子从坐标原点O沿着y轴正方向射出。射出以后，它第三次到达x轴时，与点O的距离为L。不计粒子重力，求：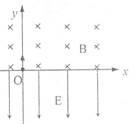
（1）粒子射出时的速度v；
（2）粒子从射出以后第三次到达x轴所用的总时间；
（3）若粒子从射出以后到第n次向下穿过x轴所用的总时间为tn，写出tn的表达式。
一带电粒子无初速度的进入一加速电场A，然后垂直进入两块平行金属板M、N形成的偏转电场中（偏转电场可视为匀强电场），如图所示。已知加速电场A板间电压为U1，M、N两板间的电压为U2，两板间的距离为d，板长为L，粒子的质量为m，电荷量为q，不计粒子受到的重力及它们之间的相互作用力。求：
（1）粒子穿过A板时速度大小v0；
（2）粒子从偏转电场射出时的侧移量y；
（3）粒子从偏转电场射出时速度的偏转角q。
如图所示，电源的总功率为40W，电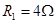阻
，
，电源内阻
，电源的输出功率为
。求：
（1）电源的内电路功率和电路中的总电流；
（2）电源的电动势；
（3）
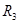的阻值。
如图，在竖直向下的磁感应强度为B的匀强磁场中，两根足够长的平行光滑金属轨道MN、PQ固定在水平面内，相距为L。一质量为m的导体棒ab垂直于MN、PQ放在轨道上，与轨道接触良好。轨道和导体棒的电阻均不计。
（1）如图1，若轨道左端接一电动势为E、内阻为r的电源和一阻值未知的电阻。闭合开关S，导体棒从静止开始运动，经过一段时间后，导体棒达到稳定最大速度vm，求此时电源的输出功率。
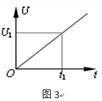
（2）如图2，若轨道左端接一电容器，电容器的电容为C，导体棒在水平恒定拉力的作用下从静止（t=0）开始向右运动。电容器两极板电势差随时间变化的图象如图3所示，已知t1时刻电容器两极板间的电势差为U1。求导体棒运动过程中受到的水平拉力大小。
