四．附加题（本小题满分8分）
设复数
与复平面
上点P(x,y)对应，且复数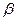
满足条件
|
a（其中n
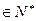.常数a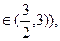
当n为奇数时
，动点P(x,y)的轨迹为C1, 当n为偶数时，动点P(x,y)的轨迹为C2,且两条曲线都经过
点D(2,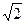
),求轨迹C1 与C2的方程？
设函数y=f(x)是定义在R+上的减函数，并且满足f(xy)=f(x)+f(y)， f(2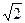
)=1，
(1).求f(1)的值;
(2).求f(8)的值.
(3).如果f(4)+f(x-2)<2,求x的取值范围。
已知函数
(1).试判断并证明该函数的奇偶性。
(2).证明函数f(x)在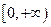
上是单调递增的。
①求函数y=x+
的值域.；
②作函数y=|-x2+2x+3|的图象，并写出它的单调区间及单调性。
已知A={1，2，x2－5x＋9}，B={3，x2＋ax＋a}，如果A={1，2，3}，2∈B，求实数a的值.
设函数
，其中
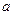为常数．
（1）证明：对任意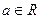
，
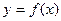的图象恒过定点；
（2）当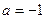
时，判断函数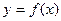是否存在极值？若存在，证明你的结论并求出所有
极值；若不存在，说明理由．