如图,正方形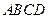 所在平面与圆
所在平面与圆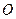 所在平面相交于
所在平面相交于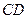 ,线段
,线段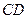 为圆
为圆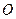 的弦,
的弦,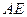 垂直于圆
垂直于圆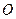 所在平面,垂足
所在平面,垂足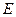 是圆
是圆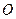 上异于
上异于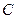 .
.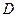 的点,
的点,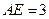 ,圆
,圆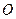 的直径为9.
的直径为9.
(I)求证:平面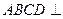 平面
平面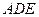 ;
;
(II)求二面角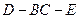 的平面角的正切值.
的平面角的正切值.
为加快新冠肺炎检测效率,某检测机构采取“ 合 1 检测法", 即将 个人的拭自样本合并检测, 若为阴性, 则可确定有样本都是阴性的; 若为阳性, 则还需要对本组的每个人再做检测. 现有 100 人, 已知其中 2 人 感染病毒.
(1) ①若采用“ 10 合 1 检测法”, 且两名感染患者在同一组, 求总检测次数.
② 已知 10 人分成一组, 分 10 组, 两名感染患者在同一组的概率为 , 定义随机变量 为总检测次数, 求检测次数 的分布列和数学期望 .
(2) 若采用“ 5 合 1 检测法”, 检测次数 的期望为 , 试比较 与 的大小(直接写出结果).
已知正方体 , 点 为 中点, 直线 交平面 于点 .

(1) 求证:点 为 中点.
(2) 若点 为棱 上一点, 且二面角 的余弦值为 , 求 .
已知在 中, .
(1) 求 的大小.
(2) 在三个条件中选择一个作为已知, 使 存在且唯一确定, 并求 边上中线的长度.
(3)① ; ② 的周长为 ; ③ 的面积为 .
已知 , 给出下列四个结论:
(1) 若 , 则 有两个零点;
(2) 存在 , 使得 有一个零点;
(3) 存在 , 使得 有三个零点;
(4) 存在 , 使得 有三个零点.
以上正确结论的序号是。
设a,b为实数,且 ,函数
(1)求函数 的单调区间;
(2)若对任意 ,函数 有两个不同的零点,求a的取值范围;
(3)当 时,证明:对任意 ,函数 有两个不同的零点 ,满足 .
(注: 是自然对数的底数)