(本小题满分12分)
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P、Q分别为AE、AB的中点.
(1)证明:PQ∥平面ACD;
(2)求AD与平面ABE所成角的正弦值.
已知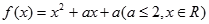 ,
, ,
,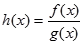
(1)当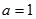 时,求
时,求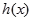 的单调区间
的单调区间
(2)若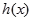 在
在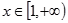 上是递减的,求实数
上是递减的,求实数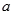 的取值范围;
的取值范围;
(3)是否存在实数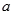 ,使
,使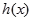 的极大值为3?若存在,求
的极大值为3?若存在,求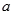 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知四棱锥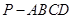 的底面为直角梯形,
的底面为直角梯形,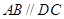 ,
,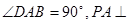 底面
底面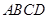 ,且
,且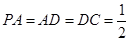 ,
,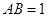 ,
,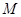 是
是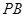 的中点.
的中点.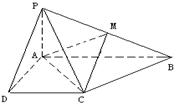
(1)证明:面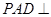 面
面 ;
;
(2)求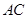 与
与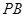 所成的角的余弦值;
所成的角的余弦值;
(3)求二面角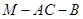 的正弦值.
的正弦值.
已知函数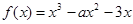 ,
,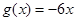 (
(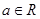 ).
).
(1)若x=3是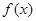 的极值点,求
的极值点,求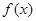 在
在 [1,a]上的最小值和最大值;
[1,a]上的最小值和最大值;
(2)若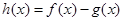 在
在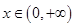 时是增函数,求实数a的取值范围.
时是增函数,求实数a的取值范围.
在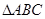 中,
中,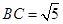 ,
,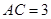 ,
,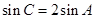 .
.
(1)求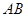 长;
长;
(2)求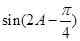 的值.
的值.
已知定义在区间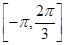 上的函数y=f(x)的图象关于直线x=-
上的函数y=f(x)的图象关于直线x=-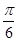 对称,当x∈
对称,当x∈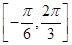 时,函数f(x)=Asin(ωx+φ)
时,函数f(x)=Asin(ωx+φ)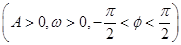 的图象如图所示.
的图象如图所示.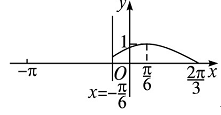
(1)求函数y=f(x)在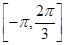 上的表达式;
上的表达式;
(2)求方程f(x)=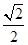 的解.
的解.