(本小题满分12分)
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD是正方形,DM⊥PC,垂足为M.
(1)求证:BD⊥平面PAC.
(2)求证:平面MBD⊥平面PCD.
已知函数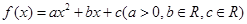
(1)若函数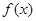 的最小值是
的最小值是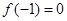 ,且
,且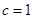 ,
,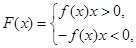 求
求 的值:
的值:
(2)若 ,且
,且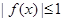 在区间
在区间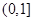 恒成立,试求
恒成立,试求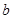 取范围;
取范围;
如图,矩形ABCD内接于半径为r的圆O,点P是圆周上任意一点,求证:PA2+PB2+PC2+PD2=8r2.
已知椭圆的中心为O,长轴、短轴的长分别为2a,2b(a>b>0),A,B分别为椭圆上的两点,且OA⊥OB,过O点作OM⊥AB交AB于点M,求点M的轨迹。
已知各项为实数的数列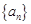 是等比数列, 且
是等比数列, 且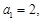
 数列
数列 满足:对任意正整数
满足:对任意正整数 ,有
,有 .
.
(1)求数列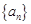 与数列
与数列 的通项公式;
的通项公式;
(2)在数列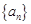 的任意相邻两项
的任意相邻两项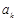 与
与 之间插入
之间插入 个
个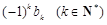 后,得到一个新的数列
后,得到一个新的数列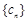 . 求数列
. 求数列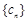 的前2012项之和.
的前2012项之和.
某校要用三辆校车从新校区把教师接到老校区,已知从新校区到老校区有两条公路,校车走公路①堵车的概率为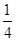 ,不堵车的概率为
,不堵车的概率为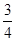 ;校车走公路②堵车的概率为
;校车走公路②堵车的概率为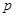 ,不堵车的概率为
,不堵车的概率为 .若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
(1)若三辆校车中恰有一辆校车被堵的概率为 ,求走公路②堵车的概率;
,求走公路②堵车的概率;
(2)在(1)的条件下,求三辆校车中被堵车辆的个数 的分布列和数学期望.
的分布列和数学期望.