设椭圆 过点
过点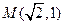 ,离心率为
,离心率为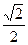
(Ⅰ)求椭圆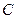 的方程;
的方程;
(Ⅱ)当过点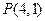 的动直线
的动直线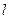 与椭圆
与椭圆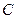 相交与两不同点
相交与两不同点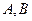 时,在线段
时,在线段 上取点
上取点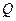 ,满足
,满足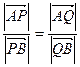 =
=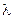 ,证明:点
,证明:点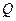 的轨迹与
的轨迹与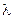 无关.
无关.
已知集合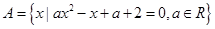 .
.
(1)若 中只有一个元素,求
中只有一个元素,求 的值,并把这个元素写出来;
的值,并把这个元素写出来;
(2)若 中至多只有一个元素,求
中至多只有一个元素,求 的取值范围.
的取值范围.
(1)计算: ;
;
(2)设 ,求
,求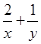 的值.
的值.
设函数 .
.
(1)若函数 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;
(2)当a=1时,求函数 在区间[t,t+3]上的最大值.
在区间[t,t+3]上的最大值.
设双曲线C: (a>0,b>0)的一个焦点坐标为(
(a>0,b>0)的一个焦点坐标为( ,0),离心率
,0),离心率 , A、B是双曲线上的两点,AB的中点M(1,2).
, A、B是双曲线上的两点,AB的中点M(1,2).
(1)求双曲线C的方程;
(2)求直线AB方程;
(3)如果线段AB的垂直平分线与双曲线交于C、D两点,那么A、B、C、D四点是否共圆?为什么?
已知数列 的前
的前 项和为
项和为 ,且满足
,且满足 .
.
(1)求 ,
, 的值;
的值;
(2)求 ;
;
(3)设 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.