(本小题满分12分)
设数列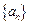 的前
的前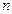 项和为
项和为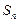 ,且满足
,且满足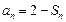
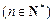 .
.
(Ⅰ)求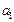 ,
,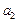 ,
,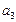 ,
, 的值并猜想这个数列的通项公式
的值并猜想这个数列的通项公式
(Ⅱ)证明数列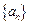 是等比数列.
是等比数列.
(本小题满分12分)数列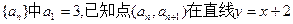 上,
上,
(I)求数列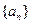 的通项公式;
的通项公式;
(II)若
如图所示,在矩形ABCD中,AB=4,AD=2 ,E是CD的中点,O为AE的中点,以AE为折痕,将△ADE向上折起,使D到P,且PC=PB
,E是CD的中点,O为AE的中点,以AE为折痕,将△ADE向上折起,使D到P,且PC=PB (1)求证:PO⊥面ABCE;
(1)求证:PO⊥面ABCE;
(2)求AC与面PAB所成角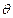 的正弦值.
的正弦值.
(本小题满分12分)某地决定新建A,B,C三类工程,A,B,C三类工程所含项目的个数分别占总项目数的 (总项目数足够多),现有3名工人独立地从中任选一个项目参与建设
(总项目数足够多),现有3名工人独立地从中任选一个项目参与建设
(Ⅰ)求他们选择的项目所属工程 类别相同的概率;
类别相同的概率;
(Ⅱ)记 为3人中选择的项目属于B类工程或C类工程的人数,求
为3人中选择的项目属于B类工程或C类工程的人数,求 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)已知函数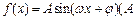 >0,
>0, >0,
>0, <
<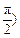 的图象与
的图象与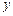 轴的交点为(0,1),它在
轴的交点为(0,1),它在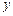 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为 和
和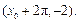
(1)写出 的解析式及
的解析式及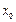 的值;(2)若锐角
的值;(2)若锐角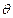 满足
满足 ,求
,求 的值.
的值.
 |
(本小题满分10分)选修4-5:不等式选讲已知对于任意非零实数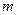 ,不等式
,不等式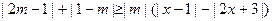 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。