已知正方体ABCD—A1B1C1D1,O是底ABCD对角线的交点。求证: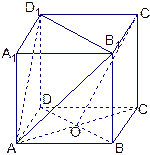
(1)
(2)C1O∥面AB1D1;
一个几何体的三视图如下图所示,已知正(主)视图是底边长为1的平行四边形,侧(左)视图是一个长为 ,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.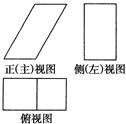
(1)求该几何体的体积V;
(2)求该几何体的表面积S.
如图,点C是以AB为直径的圆上的一点,直角梯形BCDE所在平面与圆O所在平面垂直,且DE∥BC,DC⊥BC,DE= BC.
BC.
(1)证明:EO∥平面ACD;
(2)证明:平面ACD⊥平面BCDE.
如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.
求证:(1)平面EFG∥平面ABC;(2)BC⊥SA.
已知四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.
(1)求证:BE∥平面PDA;
(2)若N为线段PB的中点,求证:NE⊥平面PDB.
如图甲,⊙O的直径AB=2,圆上两点C、D在直径AB的两侧,且∠CAB= ,∠DAB=
,∠DAB= .沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题:
.沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题:
(1)求三棱锥C-BOD的体积;
(2)求证:CB⊥DE;
(3)在 上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.
上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.