已知椭圆焦点是 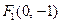 和
和 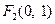 ,离必率
,离必率 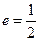
(1)求椭圆的标准方程;
(2)又设点P在这个椭圆上,且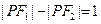 ,求
,求 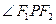 的余弦值。
的余弦值。
设
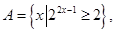
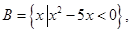 求(1)A∩B,A∪B;
求(1)A∩B,A∪B;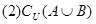
(本小题满分10分)
已知数列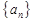 的前
的前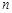 项和为
项和为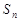 ,
,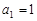 ,且
,且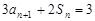 (
(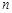 为正整数).
为正整数).
(Ⅰ)求数列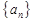 的通项公式;
的通项公式;
(Ⅱ)记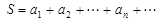 .
. 若对任意正整数
若对任意正整数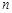 ,
,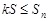 恒成立,求实数
恒成立,求实数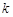 的最大值.
的最大值.
(本小题满分12分)
设函数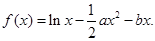
(Ⅰ)当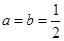 时,求
时,求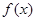 的最大值;
的最大值;
(Ⅱ)令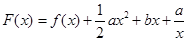 ,(
,(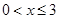 ),其图象上任意一点
),其图象上任意一点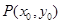 处切线的斜率
处切线的斜率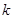 ≤
≤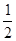 恒成立,求实数
恒成立,求实数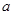 的取值范围;
的取值范围;
(本小题满分12分)
已知椭圆C: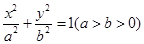 的离心率为
的离心率为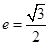 ,A,B分别为椭圆的长轴和短轴的端点,M为AB的中点,O为坐标原点,且
,A,B分别为椭圆的长轴和短轴的端点,M为AB的中点,O为坐标原点,且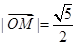 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过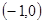 的直线
的直线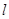 与椭圆交于P、Q两点,求
与椭圆交于P、Q两点,求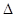 POQ的面积的最大时直线
POQ的面积的最大时直线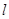 的方程。
的方程。
(本小题满分12分)
如图:梯形 和正
和正
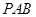 所在平面互相垂直,其中
所在平面互相垂直,其中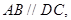
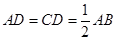 ,且
,且 为
为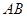 中点.
中点. 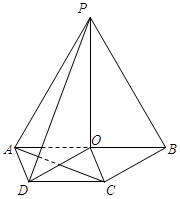
(Ⅰ) 求证: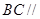 平面
平面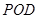 ;
;
(Ⅱ)若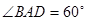 ,求二面角
,求二面角 的余弦值;
的余弦值;