为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费 用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=
用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= 若不建隔热层,每年能源消耗费用为8万元。设
若不建隔热层,每年能源消耗费用为8万元。设
f(x)为隔热层建造费用与20年的能源消耗费用之和。
(1)求k的值及f(x)的表达式
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
(本小题满分14分)
某种型号的汽车在匀速行驶中每小时的耗油量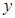 (升)关于行驶速度
(升)关于行驶速度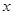 (km/h)的函数解析式可以表示为
(km/h)的函数解析式可以表示为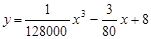
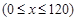 ,
,
已知甲、乙两地相距100km .
(1)当汽车以40km/h的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
(本小题满分12分)
已知数列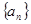 满足
满足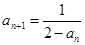 ,
, .
.
(1)计算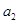 ,
,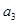 ,
,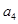 ,
, 的值;
的值;
(2)根据以上计算结果猜想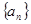 的通项公式,并用数学归纳法证明你的猜想.
的通项公式,并用数学归纳法证明你的猜想.
(本小题满分12分)已知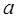 为实数,
为实数,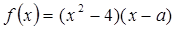
(1)求导数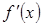 ;
;
(2)若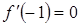 ,求
,求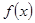 在[-2,2]上的最大值和最小值;
在[-2,2]上的最大值和最小值;
(本小题满分12分)已知复数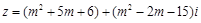 ,当实数
,当实数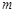 为何值时,
为何值时,
(1) 为实数;(2)
为实数;(2) 为虚数;(3)
为虚数;(3) 为纯虚数.
为纯虚数.
(本小题满分14分)
已知函数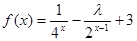 (
(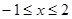 ).
).
(1)若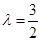 时,求函数
时,求函数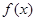 的值域;
的值域;
(2)若函数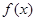 的最小值是1,求实数
的最小值是1,求实数 的值.
的值.