(本小题满分12分)已知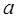 为实数,
为实数,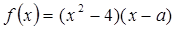
(1)求导数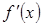 ;
;
(2)若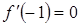 ,求
,求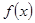 在[-2,2]上的最大值和最小值;
在[-2,2]上的最大值和最小值;
对于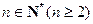 ,定义一个如下数阵:
,定义一个如下数阵: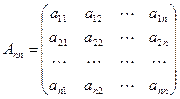
其中对任意的 ,
,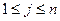 ,当
,当 能整除
能整除 时,
时,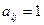 ;当
;当 不能整除
不能整除 时,
时,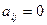 .设
.设 .
.
(Ⅰ)当 时,试写出数阵
时,试写出数阵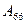 并计算
并计算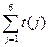 ;
;
(Ⅱ)若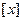 表示不超过
表示不超过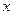 的最大整数,求证:
的最大整数,求证: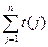
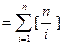 ;
;
(Ⅲ)若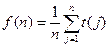 ,
, ,求证:
,求证: .
.
已知椭圆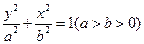 的离心率为
的离心率为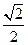 ,且两个焦点和短轴的一个端点是一个等腰三角形的顶点.斜率为
,且两个焦点和短轴的一个端点是一个等腰三角形的顶点.斜率为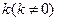 的直线
的直线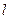 过椭圆的上焦点且与椭圆相交于
过椭圆的上焦点且与椭圆相交于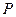 ,
, 两点,线段
两点,线段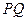 的垂直平分线与
的垂直平分线与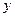 轴相交于点
轴相交于点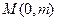 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)求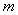 的取值范围;
的取值范围;
(Ⅲ)试用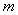 表示△
表示△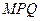 的面积,并求面积的最大值.
的面积,并求面积的最大值.
已知函数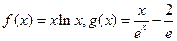 .
.
(Ⅰ)求函数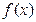 在区间
在区间 上的最小值;
上的最小值;
(Ⅱ)证明:对任意 ,都有
,都有 成立.
成立.
甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲面试合格的概率为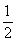 ,乙、丙面试合格的概率都是
,乙、丙面试合格的概率都是 ,且面试是否合格互不影响.
,且面试是否合格互不影响.
(Ⅰ)求至少有1人面试合格的概率;
(Ⅱ)求签约人数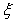 的分布列和数学期望.
的分布列和数学期望.
已知四棱锥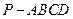 的底面是菱形.
的底面是菱形.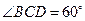 ,
,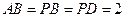 ,
,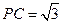 ,
,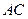 与
与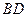 交于
交于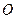 点,
点,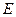 ,
,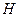 分别为
分别为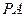 ,
,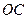 的中点.
的中点. (Ⅰ)求证:
(Ⅰ)求证: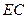 ∥平面
∥平面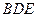 ;
;
(Ⅱ)求证: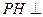 平面
平面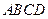 ;
;
(Ⅲ)求直线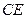 与平面
与平面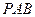 所成角的正弦值
所成角的正弦值