选修4—4:坐标系与参数方程
(本题满分l0分)
在直角坐标系 中,以O为极点,
中,以O为极点,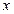 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为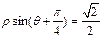 .圆O的参数方程为
.圆O的参数方程为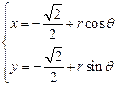 ,(
,(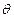 为参数,
为参数, )
)
(I)求圆心的一个极坐标;
(Ⅱ)当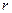 为何值时,圆O上的点到直线
为何值时,圆O上的点到直线 的最大距离为3.
的最大距离为3.
已知椭圆的顶点与双曲线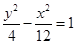 的焦点重合,它们的离心率之和为
的焦点重合,它们的离心率之和为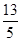 ,若椭圆的焦点在
,若椭圆的焦点在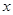 轴上,求椭圆的方程.
轴上,求椭圆的方程.
如图,在三棱锥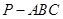 中,
中,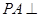 底面
底面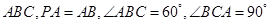 ,点
,点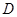 ,
, 分别在棱
分别在棱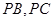 上,且
上,且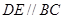
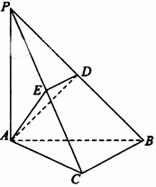
(Ⅰ)求证: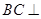 平面
平面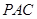 ;
;
(Ⅱ)当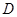 为
为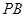 的中点时,求
的中点时,求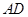 与平面
与平面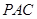 所成的角的正弦值;
所成的角的正弦值;
(Ⅲ)是否存在点 使得二面角
使得二面角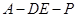 为直二面角?若存在,请确定点E的位置;若不存在,请说明理由.
为直二面角?若存在,请确定点E的位置;若不存在,请说明理由.
如图1,在平行四边形ABCD中,AB=1,BD= ,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
(1)若F、G分别是AD、BC的中点,且AB∥平面EFG,求证:CD∥平面EFG;
(2)当图1中AE+EC最小时,求图2中二面角A-EC-B的大小.
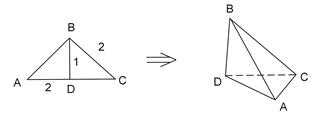
如图,在 中,
中, 为
为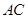 边上的高,
边上的高,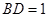 ,
,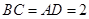 ,沿
,沿 将
将 翻折,使得
翻折,使得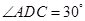 ,得到几何体
,得到几何体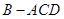 。
。
(1)求证: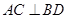 ;
;
(2)求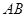 与平面
与平面 所成角的正切值。
所成角的正切值。
如图,直四棱柱ABCD—A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=0,A1C1∩B1D1=O1,E是O1A的中点.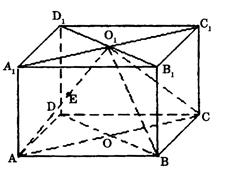
(1)求证:平面O1AC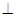 平面O1BD
平面O1BD
(2)求二面角O1-BC-D的大小;
(3)求点E到平面O1BC的距离.