(本小题满分12分)
某校高三(1)班共有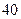 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在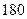 分钟到
分钟到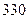 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分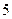 个组统计得到如下频率分布表:
个组统计得到如下频率分布表:
| 分组 |
频数 |
频率 |
| [180 , 210) |
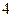 |
 |
| [210 , 240) |
 |
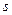 |
| [240 , 270) |
 |
 |
| [270 , 300) |
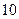 |
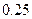 |
| [300 , 330) |
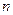 |
 |
(1)求分布表中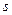 ,
, 的值;
的值;
(2)某兴趣小组为研究每天自主学习的时间与学习成绩的相关性,需要在这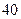 名学生中按时间用分层抽样的方法抽取
名学生中按时间用分层抽样的方法抽取 名学生进行研究,问应抽取多少名第一组的学生?
名学生进行研究,问应抽取多少名第一组的学生?
(3)已知第一组的学生中男、女生均为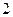 人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.
人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.
(本小题满分10分)选修4—5:不等式选讲
已知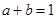 ,对
,对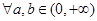 ,
, 恒成立,求
恒成立,求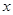 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:极坐标与参数方程选讲
已知曲线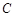 的极坐标方程是
的极坐标方程是 ,直线
,直线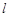 的参数方程是
的参数方程是 (
(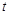 为参数).
为参数).
(Ⅰ)将曲线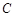 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)设直线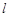 与
与 轴的交点是
轴的交点是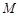 ,
,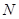 是曲线
是曲线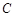 上一动点,求
上一动点,求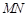 的最大值.
的最大值.
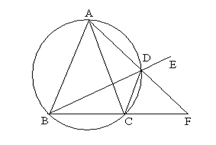
(本小题满分10分)选修4-1几何证明选讲
已知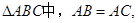
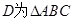 外接圆劣弧
外接圆劣弧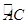 上的点(不与点
上的点(不与点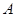 、
、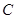 重合),延长
重合),延长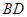 至
至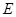 ,延长
,延长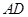 交
交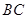 的延长线于
的延长线于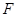 .
.
(Ⅰ)求证: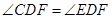 ;
;
(Ⅱ)求证: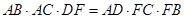 .
.
已知函数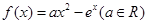
(Ⅰ)当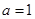 时,判断函数
时,判断函数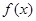 的单调区间并给予证明;
的单调区间并给予证明;
(Ⅱ)若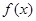 有两个极值点
有两个极值点 ,证明:
,证明: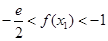 .
.
已知抛物线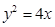 ,直线
,直线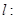
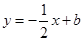 与抛物线交于
与抛物线交于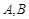 两点.
两点.
(Ⅰ)若 轴与以
轴与以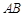 为直径的圆相切,求该圆的方程;
为直径的圆相切,求该圆的方程;
(Ⅱ)若直线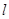 与
与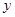 轴负半轴相交,求
轴负半轴相交,求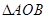 面积的最大值.
面积的最大值.