已知数列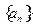 的前
的前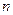 项和为
项和为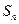 ,且
,且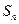 =
= ,数列
,数列 中,
中, ,点
,点 在直线
在直线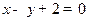 上.(I)求数列
上.(I)求数列 的通项
的通项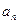 和
和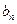 ;
;
(II) 设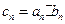 ,求数列
,求数列 的前n项和
的前n项和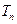 ,并求满足
,并求满足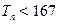 的最大正整数
的最大正整数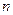 .
.
已知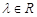 ,函数
,函数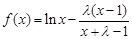 ,其中
,其中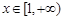 .
.
(Ⅰ)当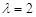 时,求
时,求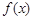 的最小值;
的最小值;
(Ⅱ)在函数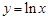 的图像上取点
的图像上取点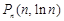
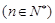 ,记线段PnPn+1的斜率为kn ,
,记线段PnPn+1的斜率为kn ,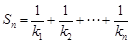 .对任意正整数n,试证明:
.对任意正整数n,试证明:
(ⅰ)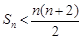 ;
;
(ⅱ)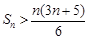 .
.
如图,实线部分的月牙形公园是由圆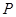 上的一段优弧和圆
上的一段优弧和圆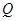 上的一段劣弧围成,圆
上的一段劣弧围成,圆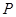 和圆
和圆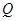 的半径都是
的半径都是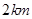 ,点
,点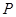 在圆
在圆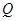 上,现要在公园内建一块顶点都在圆
上,现要在公园内建一块顶点都在圆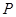 上的多边形活动场地.
上的多边形活动场地.

(Ⅰ)如图甲,要建的活动场地为△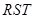 ,求活动场地的最大面积;
,求活动场地的最大面积;
(Ⅱ)如图乙,要建的活动场地为等腰梯形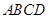 ,求活动场地的最大面积;
,求活动场地的最大面积;
如图,点P(0,−1)是椭圆C1: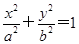 (a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.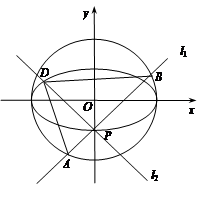
(Ⅰ)求椭圆C1的方程;
(Ⅱ)求△ABD面积取最大值时直线l1的方程.
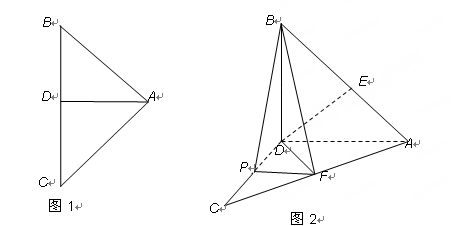
如图1,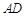 是直角△
是直角△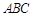 斜边上的高,沿
斜边上的高,沿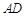 把△
把△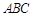 的两部分折成直二面角(如图2),
的两部分折成直二面角(如图2),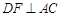 于
于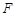 .
.
(Ⅰ)证明: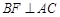 ;
;
(Ⅱ)设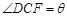 ,
,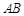 与平面
与平面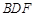 所成的角为
所成的角为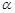 ,二面角
,二面角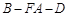 的大小为
的大小为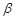 ,试用
,试用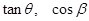 表示
表示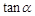 ;
;
(Ⅲ)设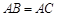 ,
,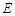 为
为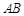 的中点,在线段
的中点,在线段 上是否存在一点
上是否存在一点 ,使得
,使得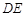 ∥平面
∥平面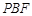 ?若存在,求
?若存在,求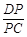 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
一个袋子中装有6个红球和4个白球,假设袋子中的每一个球被摸到可能性是相等的。
(Ⅰ)从袋子中任意摸出3个球,求摸出的球均为白球的概率;
(Ⅱ)一次从袋子中任意摸出3个球,若其中红球的个数多于白球的个数,则称“摸球成功”(每次操作完成后将球放回),某人连续摸了3次,记“摸球成功”的次数为 ,求
,求 的分布列和数学期望。
的分布列和数学期望。