(本小题共13分)
已知函数 .
.
(Ⅰ)若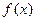 在
在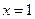 处取得极值,求a的值;
处取得极值,求a的值;
(Ⅱ)求函数 在
在 上的最大值.
上的最大值.
给出下列四个结论:
(1)如图 中,
中,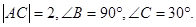 D是斜边AC上的点,|CD|=|CB|.以B为起点任作一条射线BE交AC于E点,则E点落在线段CD上的概率是
D是斜边AC上的点,|CD|=|CB|.以B为起点任作一条射线BE交AC于E点,则E点落在线段CD上的概率是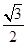 ;
;
(2)设某大学的女生体重y(kg)与身高x(cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2, ,n),用最小二乘法建立的线性回归方程为 ,则若该大学某女生身高增加1 cm,则其体重约增加0.85 kg;
,则若该大学某女生身高增加1 cm,则其体重约增加0.85 kg;
(3)为调查中学生近视情况,测得某校男生150名中有80名近视,在140名女生中有70名近视.在检验这些学生眼睛近视是否与性别有关时,应该用独立性检验最有说服力;
(4)已知随机变量 服从正态分布
服从正态分布 则
则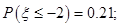
其中正确结论的个数为()
| A.1 | B.2 | C.3 | D.4 |
(本小题满分10分) 已知数列 通项公式为
通项公式为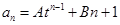 ,其中
,其中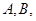
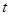 为常数,且
为常数,且 ,
, .等式
.等式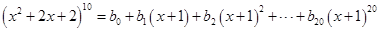 ,其中
,其中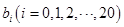 为实常数.
为实常数.
(1)若 ,求
,求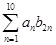 的值;
的值;
(2)若 ,且
,且 ,求实数
,求实数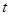 的值.
的值.
(本小题满分10分)如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AP=1,AD=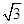 ,E为线段PD上一点,记
,E为线段PD上一点,记 .当
.当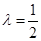 时,二面角
时,二面角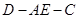 的平面角的余弦值为
的平面角的余弦值为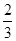 .
.
(1)求AB的长;
(2)当 时,求直线BP与直线CE所成角的余弦值.
时,求直线BP与直线CE所成角的余弦值.
(本小题满分10分,不等式选讲)
已知实数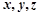 满足
满足 ,求
,求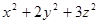 的最小值.
的最小值.
(本小题满分10分,坐标系与参数方程选讲)
在平面直角坐标系xOy中,已知直线 的参数方程为:
的参数方程为: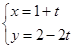 (t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2cosθ.直线
(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2cosθ.直线 与圆相交于A,B两点,求线段AB的长.
与圆相交于A,B两点,求线段AB的长.