设函数 .
.
(1)、当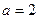 时,用函数单调性定义求
时,用函数单调性定义求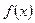 的单调递减区间
的单调递减区间
(2)、若连续掷两次骰子(骰子六个面上分别标以数字1,2,3,4,5,6)得到的点数 分别作为
分别作为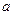 和
和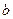 ,求
,求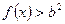 恒成立的概率;
恒成立的概率;
围建一个面积为360㎡的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修),其它三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2m的进出 口,如图所示。已知旧墙的维修费用为45元/m ,新墙的造价为180元/m ,设利用的旧墙的长度为
口,如图所示。已知旧墙的维修费用为45元/m ,新墙的造价为180元/m ,设利用的旧墙的长度为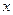 (单位:m), 修建此矩形场地围墙的总费用为
(单位:m), 修建此矩形场地围墙的总费用为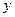 (单位:元)。
(单位:元)。
(1)将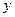 表示为
表示为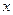 的函数;
的函数;
(2)试确定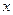 ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
已知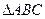 的内角
的内角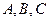 所对的边分别为
所对的边分别为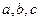 ,且
,且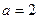 ,
,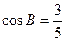 ,
,
(1)若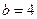 ,求
,求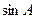 的值;
的值;
(2)若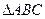 的面积
的面积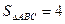 , 求
, 求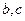 的值。
的值。
记等比数列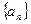 的前
的前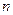 项和为
项和为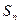 ,已知
,已知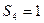 ,
,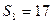 , 求数列
, 求数列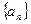 的通项公式。
的通项公式。
(.利用“五点法”画出函数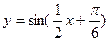 在长度为一个周期的闭区间的简图
在长度为一个周期的闭区间的简图
(2)并说明该函数图象可由y=sinx(x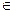 R)的图象经过怎样平移和伸缩变换得到的。
R)的图象经过怎样平移和伸缩变换得到的。
(.已知函数y=Asin(ωx+φ)+b(A>0,|φ|<π,b为常数)的 一段图象(如图)所示.
①求函数的解析式;
②求这个函数的单调区间.