甲乙两人各有相同的小球10个，在每人的10个小球
中都有5个标有数字1，3个标有数字2，2个标有数字3。两人同时分别从自己的小球中任意抽取1个，规定：若抽取的两个小球上的数字相同，则甲获胜，否则乙获胜，求乙获胜的概率。
在梯形ABCD中，AD∥BC，BC=2AD，AD=AB=
，AB⊥BC，如图把△ABD沿BD翻折，使得平面ABD⊥平面BCD．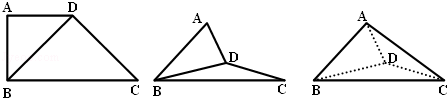
（Ⅰ）求证：CD⊥平面ABD；
（Ⅱ）若点M为线段BC中点，求点M到平面ACD的距离．
已知{an}是正项数列，a1=1，且点（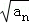
，an+1）（n∈N*）在函数y=x2+1的图象上．
（1）求数列{an}的通项公式；
（2）若列数{bn}满足b1=1，bn+1=bn+2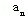
，求证：bnbn+2＜b
．
设△ABC的内角A、B、C所对边的长分别为a、b、c，且有2sinBcosA=sinAcosC+cosAsinC．
（Ⅰ）求角A的大小；
（Ⅱ）若b=2，c=1，D为BC的中点，求AD的长．
设a为实数，函数f（x）=ex﹣2x+2a，x∈R．
（1）求f（x）的单调区间及极值；
（2）求证：当a＞ln2﹣1且x＞0时，ex＞x2﹣2ax+1．
在正项数列{an}中，a1=1，点An（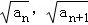
）在曲线y2﹣x2=1上，数列{bn}中，点（bn，Tn）在直线y=﹣
x+1上，其中Tn是数列{bn}的前n项和．
（1）求数列{an}，{bn}的通项公式an，bn；
（2）若cn=an•bn，数列{cn}的前n项和Sn．