在数列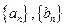 中,
中, 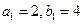 ,且
,且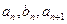 成等差数列,
成等差数列, 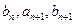 成等比数列
成等比数列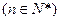 .
.
(1)求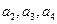 及
及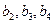 ,由此猜测
,由此猜测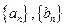 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(2)证明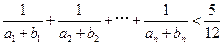 .
.
(本小题满分12分)已知函数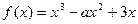
(1)若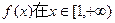 上增函数,求实数a的取值范围;
上增函数,求实数a的取值范围;
(2)若x=3是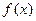 的极值点,求
的极值点,求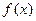 在
在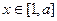 上的最小值和最大值.
上的最小值和最大值.
(本小题满分12分)已知△ABC中,A、B、C所对的边分别为a、b、c,当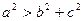 且
且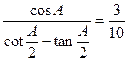 时,求sin2A的值.
时,求sin2A的值.
(本小题满分14分)
设数列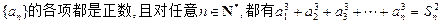 ,
,
其中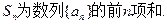
(I)求证: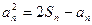 ;
;
(II)求数列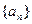 的通项公式;
的通项公式;
(III)设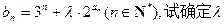 的取值范围,使得对任意
的取值范围,使得对任意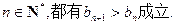
(本小题满分12分)
已知函数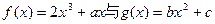 的图像都过点P(2,0),且在点P处
的图像都过点P(2,0),且在点P处
有相同的切线。
(I)求实数a、b、c的值;
(II)设函数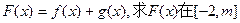 上的最小值。
上的最小值。
(本小题满分12分)
某客运公司争取到一个相距100海里的甲、乙两地的客运航线权。已知轮船的平均载客人数为200人,轮船每小时使用的燃料费和轮船航行速度的平方成正比,轮船的最大速度为20海里/小时,当船速为10海里/小时,它的燃料费用是每小时60元,其余费用(不论速度如何)总计是每小时150元,假定轮船从甲地到乙地匀速航行。
(I)求轮船每小时的燃料费W与速度v的关系式;
(II)若公司打算从每位乘客身上获得利润10元,那么该公司设计的船票价格最低可以是多少?(精确到1元,参考数据: )
)