设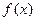 是定义在[-1,1]上的奇函数,且对任意
是定义在[-1,1]上的奇函数,且对任意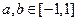 ,当
,当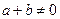 时,都有
时,都有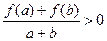 .
.
(1)若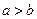 ,试比较
,试比较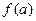 与
与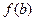 的大小;
的大小;
(2)解不等式
(3)如果 和
和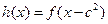 这两个函数的定义域的交集为空集,求
这两个函数的定义域的交集为空集,求 的取值范围.
的取值范围.
如图所示,在直四棱柱 中,
中,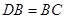 ,
, ,点
,点 是棱
是棱 上的一点.
上的一点.
(1)求证: 平面
平面 ;
;
(2)求证: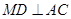 ;
;
(3)是否存在点 ,使得平面
,使得平面 ⊥平面
⊥平面 ?若存在,试确定点
?若存在,试确定点 的位置,并给出证明;若不存在,说明理由.
的位置,并给出证明;若不存在,说明理由.
如图(1)所示,在梯形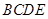 中,
中, ,
,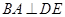 ,且
,且 ,如图(2)沿
,如图(2)沿 将四边形
将四边形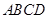 折起,使得平面
折起,使得平面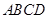 与平面
与平面 垂直,
垂直, 为
为 的中点.
的中点.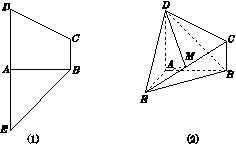
(1) 求证:平面 平面
平面 ;
;
(2) 求三棱锥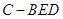 的体积.
的体积.
(3)求二面角 的正切值
的正切值
一个正方体的平面展开图及该正方体的直观图的示意图如图所示.
(1)请把字母 标记在正方体相应的顶点处(不需要说明理由)
标记在正方体相应的顶点处(不需要说明理由)
(2)判断平面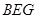 与平面
与平面 的位置关系.并证明你的结论.
的位置关系.并证明你的结论.
(3)证明:直线
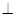 平面
平面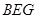
如图,四边形 与四边形
与四边形 都是梯形,
都是梯形, ,
,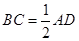 ,
, ,
, ,
,  是
是 的中点.
的中点.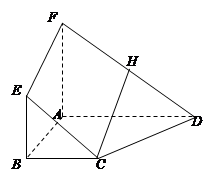
(1)证明: 平面
平面 ;
;
(2)判断 、
、 、
、 、
、 四点是否共面,并说明理由.
四点是否共面,并说明理由.
已知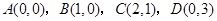 ,将四边形
,将四边形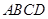 绕
绕 轴旋转一周,求所得旋转体的表面积和体积.
轴旋转一周,求所得旋转体的表面积和体积.