在棱长为1的正方体
中，
分别是
的中点，
在棱
上，且
，H为
的中点，应用空间向量方法求解下列问题.
（1）求证：
;
（2）求EF与所成的角的余弦;
（3）求FH的长.
(10分)解不等式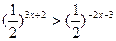 
(14分)已知圆M过定点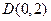
，圆心M在二次曲线
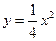上运动（1）若圆M与y轴相切，求圆M方程;(2) 已知圆M的圆心M在第一象限, 半径为
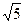,动点
是圆M外一点,过点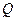
与圆M相切的切线的长为3,求动点的轨迹方程;（3）若圆M与x轴交于A，B两点，设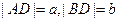
，求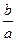
的取值范围？
在正三角形ABC中，E、F、P分别是AB、AC、BC边上的点，满足AE:EB＝CF:FA＝CP:PB＝1:2（如图1）。将△AEF沿EF折起到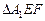
的位置，使二面角A1－EF－B成直二面角，连结A1B、A1P（如图2）
（Ⅰ）求证：A1E⊥平面BEP；
（Ⅱ）求二面角A1－BP－E的大小。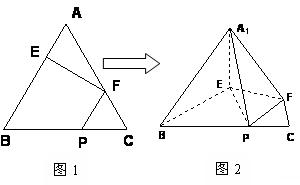
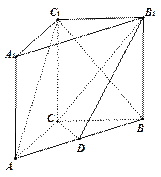
已知三棱柱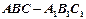
的三视图如图所示，
其中正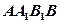视图
和侧视图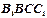
均为矩形，俯视图
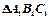中，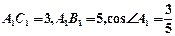
。
（I）在三棱柱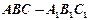
中，求证：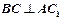
；
（II）在三棱柱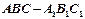
中，若
是底边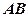
的中点，求证：
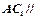平面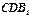
；
(10分)已知圆C与圆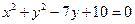
相交，所得公共弦平行于已知直线
，又圆C经过点A（-2，3），B（1，4），求圆C的方程。