(本小题满分12分)
在直角坐标 系
系 中,以
中,以 为极点,
为极点,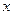 正半轴为极轴建立极坐标系,曲线
正半轴为极轴建立极坐标系,曲线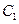 的极坐标方程为
的极坐标方程为 ,
, 分别为
分别为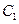 与
与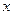 轴,
轴, 轴的交点。曲线
轴的交点。曲线 的参数方程为
的参数方程为 (
( 为参数)。
为参数)。
(1)求 的极坐标,并写出
的极坐标,并写出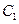 的直角坐标
的直角坐标 方程;
方程;
(2)求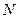 点与曲线
点与曲线 上的动点距离的最大值。
上的动点距离的最大值。
对一批共50件的某电器进行分类检测,其重量(克)统计如下:
| 重量段 |
[80,85) |
[85,90) |
[90,95) |
[95,100] |
| 件数 |
5 |
a |
15 |
b |
规定重量在82克及以下的为“A”型,重量在85克及以上的为“B”型,已知该批电器有“A”型2件
(1)从该批电器中任选1件,求其为“B”型的概率;
(2)从重量在[80,85)的5件电器中,任选2件,求其中恰有1件为“A”型的概率.
如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
(1)求证: EC⊥CD;
(2)求证:AG∥平面BDE;
(3)求:几何体EG-ABCD的体积.
已知函数 (
( )的最小正周期为
)的最小正周期为 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)将函数 的图象向左平移
的图象向左平移 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数 的图象;若
的图象;若 在
在 上至少含有10个零点,求b的最小值.
上至少含有10个零点,求b的最小值.
如图;.已知椭圆C: 的离心率为
的离心率为 ,以椭圆的左顶点T为圆心作圆T:
,以椭圆的左顶点T为圆心作圆T: 设圆T与椭圆C交于点M、N.
设圆T与椭圆C交于点M、N.
(1)求椭圆C的方程;
(2)求 的最小值,并求此时圆T的方程;
的最小值,并求此时圆T的方程;
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与 轴交于点R,S,O为坐标原点. 试问;是否存在使
轴交于点R,S,O为坐标原点. 试问;是否存在使 最大的点P,若存在求出P点的坐标,若不存在说明理由.
最大的点P,若存在求出P点的坐标,若不存在说明理由.
已知函数 ,其中
,其中 ,
, 是自然对数的底数.
是自然对数的底数.
(1)求函数 的零点;
的零点;
(2)若对任意 均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
(3)已知 ,且函数
,且函数 在R上是单调函数,探究函数
在R上是单调函数,探究函数 的单调性.
的单调性.