(本小题满分12分)
某班主任对全班50名学生进行了作业量
多少的调查。数据如下表：
| |
认为作业多 |
认为作业不多 |
合计 |
| 喜欢玩游戏 |
18 |
9 |
|
| 不喜欢玩游戏 |
8 |
15 |
|
| 合计 |
|
|
|
(Ⅰ) 请完善上表中的所缺的有关数据;
(Ⅱ) 试通过计算说明能有多大的把握认为喜欢玩游戏与作业量的多少有关系？
已知某几何体的俯视图是如图所示矩形．主视图是一个底边长为8、高为4的等腰三角形，左视图是一个底边长为6、高为4的等腰三角形．
（1）判断该几何体形状；
（2）求该几何体的的体积V与侧面积S．
已知
求
的取值范围．
已知f（x）=x|x﹣a|+b，x∈R．
（1）当a=1，b=1时．f（2x）=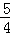
，求x的值；
（2）若b＜0，b为常数，任意x∈[0，1]，不等式f（x）＜0恒成立，求实数a的取值范围．
已知函数f（x）=x2﹣2ax+a+2，
（1）若f（x）≤0的解集A⊆[0，3]，求实数a的取值范围；
（2）若g（x）=f（x）+|x2﹣1|在区间（0，3）内有两个零点x1，x2（x1＜x2），求实数a的取值范围．
设a，b，c分别是△ABC中角A，B，C的对边
（1）若AB边上的中线CM=AB=2，求a+b的最大值；
（2）若AB边上的高h=
，求
的取值范围．