提高过江大桥的车辆通行能力可改善整个城市的交通状况。在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数。当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当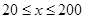 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
(Ⅰ)当 时,求函数
时,求函数 的表达式;
的表达式;
(Ⅱ)当车流密度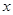 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).
设函数 ,其中
,其中 .
.
(I)若函数 图象恒过定点P,且点P关于直线
图象恒过定点P,且点P关于直线 的对称点在
的对称点在 的图象上,求m的值;
的图象上,求m的值;
(Ⅱ)当 时,设
时,设 ,讨论
,讨论 的单调性;
的单调性;
(Ⅲ)在(I)的条件下,设 ,曲线
,曲线 上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
已知数列 满足:
满足: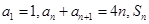 是数列
是数列 的前n项和.数列
的前n项和.数列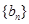 前n项的积为
前n项的积为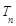 ,且
,且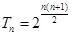
(Ⅰ)求数列 ,
,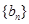 的通项公式;
的通项公式;
(Ⅱ)是否存在常数a,使得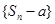 成等差数列?若存在,求出a,若不存在,说明理由;
成等差数列?若存在,求出a,若不存在,说明理由;
(Ⅲ)是否存在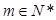 ,满足对任意自然数
,满足对任意自然数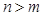 时,
时, 恒成立,若存在,求出m的值;若不存在,说明理由.
恒成立,若存在,求出m的值;若不存在,说明理由.
湖南省环保研究所对长沙市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数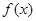 与时刻x的关系为
与时刻x的关系为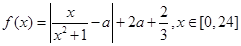 ,其中a是与气象有关的参数,且
,其中a是与气象有关的参数,且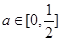 ,若用每天
,若用每天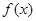 的最大值作为当天的综合放射性污染指数,并记作
的最大值作为当天的综合放射性污染指数,并记作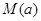 .
.
(Ⅰ)令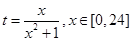 ,求t的取值范围;
,求t的取值范围;
(Ⅱ)省政府规定,每天的综合放射性污染指数不得超过2,试问目前市中心的综合放射性污染指数是否超标?
如图,在三棱柱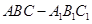 中,侧面
中,侧面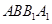 ,
,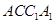 均为正方形,∠
均为正方形,∠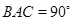 ,点
,点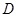 是棱
是棱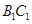 的中点.
的中点.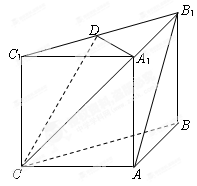
(Ⅰ)求证: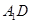 ⊥平面
⊥平面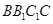 ;
;
(Ⅱ)求证: 平面
平面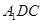 ;
;
(Ⅲ)求二面角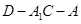 的余弦值.
的余弦值.
已知x=1是函数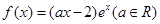 的一个极值点,
的一个极值点,
(Ⅰ)求a的值;
(Ⅱ)当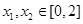 时,证明:
时,证明: