(本小题满分13分)
设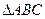 的BC边上的高AD=BC,a,b,c分别是内角A,B,C的对边。
的BC边上的高AD=BC,a,b,c分别是内角A,B,C的对边。
(1)求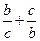 的最小值及取得最小值时
的最小值及取得最小值时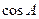 的值;
的值;
(2)把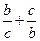 表示为
表示为 的形式,判断
的形式,判断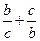 能否等于
能否等于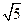 ?并说明理由。
?并说明理由。
(本小题满分13分)如图,在三棱柱ABC—A1B1C1中,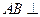 侧面BB1C1C,已知AB=BC=1,BB1=2,
侧面BB1C1C,已知AB=BC=1,BB1=2,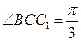 ,E为CC1的中点。
,E为CC1的中点。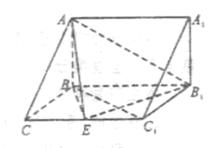
(1)求证: 平面ABC;
平面ABC;
(2)求二面角A—B1E—B的大小。
(本小题满分12分)
已知等比数列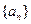 的公比是q,且
的公比是q,且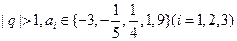
(1)求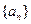 的通项公式;
的通项公式;
(2)若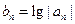 ,求数列
,求数列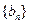 的前n项和
的前n项和
(本小题满分12分)
已知向量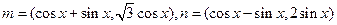 ,若函数
,若函数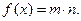
(1)求函数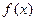 的单调递增区间;
的单调递增区间;
(2)在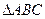 中,a,b,c分别是内角A,B,C的对边,且
中,a,b,c分别是内角A,B,C的对边,且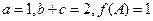 ,求角A、B、C的大小。
,求角A、B、C的大小。
(本题满分14分) 设函数f (x)=ln x+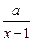 在(0,
在(0,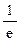 ) 内有极值.
) 内有极值.
(Ⅰ) 求实数a的取值范围;
(Ⅱ) 若x1∈(0,1),x2∈(1,+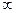 ).求证:f (x2)-f (x1)>e+2-
).求证:f (x2)-f (x1)>e+2-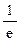 .
.
注:e是自然对数的底数.