已知 ,且正整数n满足
,且正整数n满足 ,
,
(1)求n ;
(2)若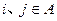 ,是否存在
,是否存在 ,当
,当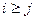 时,
时,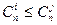 恒成立。若存在,求出最小的
恒成立。若存在,求出最小的 ;
;
若不存在,试说明理由。
(3)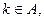 若
若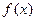 的展开式有且只有三个有理项,求
的展开式有且只有三个有理项,求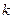 。
。
设函数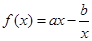 ,曲线
,曲线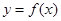 在点
在点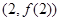 处的切线方程为
处的切线方程为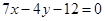 .
.
(1)求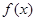 的解析式;(2)证明:曲线
的解析式;(2)证明:曲线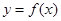 上任一点处的切线与直线
上任一点处的切线与直线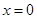 和直线
和直线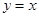 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.
本题满分10分)已知由曲线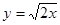 ,直线
,直线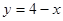 以及x轴所围成的图形的面积为S. (1)画出图像 (2)求面积S
以及x轴所围成的图形的面积为S. (1)画出图像 (2)求面积S
设命题p:实数x满足x2-4ax+3a2<0,其中a>0,
命题q:实数x满足
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)非p是非q的充分不必要条件,求实数a的取值范围.
(本小题满分14分)
设函数 .
.
(1)如果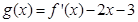 在
在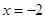 处取得最小值
处取得最小值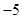 ,求函数
,求函数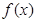 的解析式;
的解析式;
(2)如果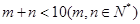 ,且
,且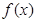 的单调递减区间的长度是正整数,试求
的单调递减区间的长度是正整数,试求 和
和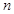 的值.(注:区间
的值.(注:区间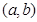 的长度为
的长度为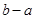 )
)
(本小题满分12分)
如图所示为一个几何体的直观图、三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).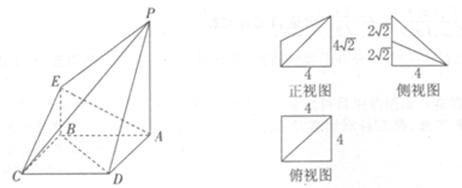
(1)求四棱锥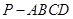 的体积;
的体积;
(2)证明: 平面
平面 ;
;
(3)若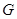 为
为 上的动点,求证:
上的动点,求证: .
.