((本题15分)
在平面直角坐标系xOy中,已知点A(0,0),B(-2,0),C(-2,1)。设k为非零实数,矩阵M=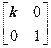 ,N=
,N=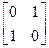 ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,
(1)求k的值。
(2)判断变换MN是否可逆,如果可逆,求矩阵MN的逆矩阵;如不可逆,说明理由.
进货原价为80元的商品400个,按90元一个售出时,可全部卖出。已知这种商品每个涨价一元,其销售数就减少20个,问售价应为多少时所获得利润最大?
三棱锥P-ABC中,三侧棱PA、PB、PC两两相互垂直,三侧面面积分
别为S1、S2、S3,底面积为S,三侧面与底面分别成角α、β、γ,(1)求S(用S1、S2、S3表示);(2)求证:cos2α+cos2β+cos2γ=1;
过点S引三条长度相等不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,
∠BSC=90°,求证:平面ABC⊥平面BSC。
如图,四棱锥V-ABCD中,∠BCD=∠BAD=90°,又∠BCV=∠BAV=90°,
求证:VD⊥AC;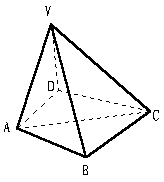
如图,正方体ABCD-A1B1C1D1的棱长为8cm,M、N、P分别是AB、A1D1、BB1的中点;(1)画出过M、N、P三点的平面与平面A1B1C1D1的交线以及与平面BB1C1C的交线;(2)设过M、N、P三点的平面与B1C1交于点Q,求PQ的长; 