((本题15分)
两个人射击,甲射击一次中靶概率是 ,乙射击一次中靶概率是
,乙射击一次中靶概率是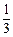 ,
,
(1)两人各射击一次,中靶至少一次就算完成目标,则完成目标概率是多少?
(2)两人各射击2次,中靶至少3次就算完成目标,则完成目标的概率是多少?
(3)两人各射击5次,是否有99%的把握断定他们至少中靶一次?
(本小题满分13 分)已知函数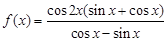 .
.
(1)求函数 的定义域;
的定义域;
(2)求函数 的单调增区间.
的单调增区间.
(本小题满分13 分)无穷数列  :
: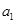 ,
,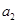 ,……,
,……, ,……,满足
,……,满足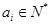 ,且
,且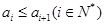 ,对于数列
,对于数列 ,记
,记 ,其中
,其中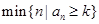 表示集合
表示集合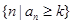 中最小的数.
中最小的数.
(1)若数列 :1,3,4,7,……,写出
:1,3,4,7,……,写出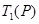 ,
,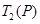 ,……,
,……,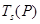 ;
;
(2)若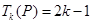 ,求数列
,求数列 前
前 项的和;
项的和;
(3)已知 ,求
,求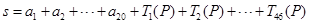 的值.
的值.
(本小题满分14 分)设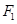 ,
,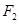 分别为椭圆
分别为椭圆 :
: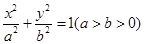 的左、右焦点,点
的左、右焦点,点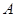 为椭圆
为椭圆 的左顶点,点
的左顶点,点 为椭圆
为椭圆 的上顶点,且
的上顶点,且 .
.
(1)若椭圆 的离心率为
的离心率为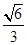 ,求椭圆
,求椭圆 的方程;
的方程;
(2)设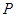 为椭圆
为椭圆 上一点,且在第一象限内,直线
上一点,且在第一象限内,直线 与
与 轴相交于点
轴相交于点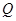 ,若以
,若以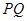 为
为
直径的圆经过点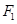 ,证明:
,证明: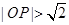
(本小题满分13分)已知函数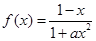 ,其中
,其中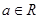 .
.
(1)当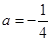 时,求
时,求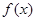 的单调区间;
的单调区间;
(2)当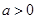 时,证明:存在实数
时,证明:存在实数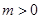 ,使得对于任意的实数
,使得对于任意的实数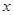 ,都有
,都有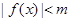 成立.
成立.
(本小题满分14 分)如图1,在边长为4的菱形 中,
中, ,
, 于点
于点 ,将
,将 沿
沿 折起到
折起到 的位置,使
的位置,使 ,如图 2.
,如图 2.

(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)判断在线段 上是否存在一点
上是否存在一点 ,使平面
,使平面 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.