(本小题满分12分)
如图,P是正三角形ABC所在平面外一点,M、N分别是AB和PC的中点,且PA=PB=PC=AB=a。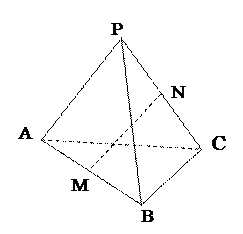
(1)求证:MN是AB和PC的公垂线
(2)求异面直线AB和PC之间的距离
已知函数 (
( ),
), .
.
(Ⅰ)若曲线 与
与 在它们的交点
在它们的交点 处具有公共切线,求
处具有公共切线,求 的值;
的值;
(Ⅱ)当 时,求函数
时,求函数 在区间
在区间 上的最大值.
上的最大值.
有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的 列联表:已知从全部210人中随机抽取1人为优秀的概率为
列联表:已知从全部210人中随机抽取1人为优秀的概率为 .
.
| 优秀 |
非优秀 |
总计 |
|
| 甲班 |
20 |
||
| 乙班 |
60 |
||
| 合计 |
210 |
(Ⅰ)请完成上面的 列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
(Ⅱ)从全部210人中有放回抽取3次,每次抽取1人,记被抽取的3人中的优秀人数为 ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求 的分布列及数学期望
的分布列及数学期望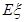 .
.
如图,直三棱柱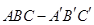 ,
,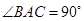 ,
,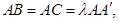 点M,N分别为
点M,N分别为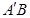 和
和 的中点.
的中点.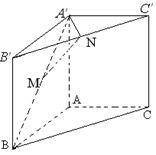
(Ⅰ)证明: ∥平面
∥平面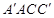 ;
;
(Ⅱ)若二面角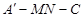 A为直二面角,求
A为直二面角,求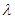 的值.
的值.
已知锐角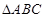 中的内角
中的内角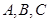 的对边分别为
的对边分别为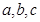 ,定义向量
,定义向量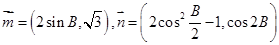 ,且
,且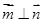 .
.
(Ⅰ)求角B的值;
(Ⅱ)如果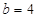 ,求
,求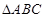 的面积的最大值.
的面积的最大值.
已知数列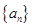 的各项都是正数,前
的各项都是正数,前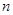 项和是
项和是 ,且点
,且点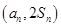 在函数
在函数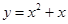 的图像上.
的图像上.
(Ⅰ)求数列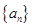 的通项公式;
的通项公式;
(Ⅱ)设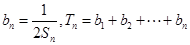 ,求
,求 .
.