本小题满分12分)
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组 ,第二组
,第二组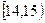 ……第五组
……第五组 ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
(Ⅰ)求这组数据的众数和中位数(精确到0.1);
(II)设 表示样本中两个学生的百米测
表示样本中两个学生的百米测
试成绩,已知
求事件“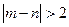 ”的概率.
”的概率.
(Ⅲ) 根据有关规定,成绩小于16秒为达标.
如果男女生使用相同的达标标准,则男女生达标情况如下 表
表
| 性别 是否达标 |
男 |
女 |
合计 |
| 达标 |
 |
 ______ ______ |
_____ |
| 不达标 |
 _____ _____ |
 |
_____ |
| 合计 |
______ |
______ |
 |
根据上表数据,能否有99%的把握认为“体育达标与性别有关”?若有,你能否提出一个更好的解决方法来?
(本小题满分12分) 中内角
中内角 的对边分别为
的对边分别为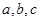 ,向量
,向量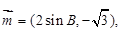
 且
且
(1)求锐角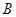 的大小;
的大小;
(2)如果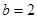 ,求
,求 的面积
的面积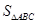 的最大值.
的最大值.
给出下列四个结论:
(1)如图 中,
中,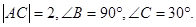 D是斜边AC上的点,|CD|=|CB|.以B为起点任作一条射线BE交AC于E点,则E点落在线段CD上的概率是
D是斜边AC上的点,|CD|=|CB|.以B为起点任作一条射线BE交AC于E点,则E点落在线段CD上的概率是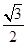 ;
;
(2)设某大学的女生体重y(kg)与身高x(cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2, ,n),用最小二乘法建立的线性回归方程为 ,则若该大学某女生身高增加1 cm,则其体重约增加0.85 kg;
,则若该大学某女生身高增加1 cm,则其体重约增加0.85 kg;
(3)为调查中学生近视情况,测得某校男生150名中有80名近视,在140名女生中有70名近视.在检验这些学生眼睛近视是否与性别有关时,应该用独立性检验最有说服力;
(4)已知随机变量 服从正态分布
服从正态分布 则
则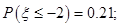
其中正确结论的个数为()
| A.1 | B.2 | C.3 | D.4 |
(本小题满分10分) 已知数列 通项公式为
通项公式为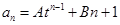 ,其中
,其中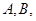
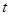 为常数,且
为常数,且 ,
, .等式
.等式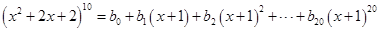 ,其中
,其中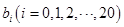 为实常数.
为实常数.
(1)若 ,求
,求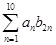 的值;
的值;
(2)若 ,且
,且 ,求实数
,求实数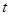 的值.
的值.
(本小题满分10分)如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AP=1,AD=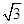 ,E为线段PD上一点,记
,E为线段PD上一点,记 .当
.当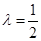 时,二面角
时,二面角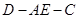 的平面角的余弦值为
的平面角的余弦值为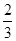 .
.
(1)求AB的长;
(2)当 时,求直线BP与直线CE所成角的余弦值.
时,求直线BP与直线CE所成角的余弦值.
(本小题满分10分,不等式选讲)
已知实数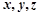 满足
满足 ,求
,求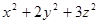 的最小值.
的最小值.