(本小题满分12分)
已知函数 ,
,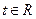 .
.
(Ⅰ)若函数 依次在
依次在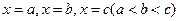 处取到极值.
处取到极值.
(ⅰ)求 的取值范围;
的取值范围;
(ⅱ)若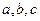 成等差数列,求
成等差数列,求 的值
的值 .
.
(Ⅱ)当 时
时 ,对任意的
,对任意的 ,不等式
,不等式 恒成立.求正整数
恒成立.求正整数 的最大值.
的最大值.
(满分12分)设f (x) 是定义在 [-1,1] 上的偶函数,f (x) 与g(x) 的图象关于x =" 1" 对称,且当x Î [2,3] 时,g(x) = a (x-2)-2 (x-2) 3(a 为常数). (Ⅰ)求f (x) 的解析式;
(Ⅰ)求f (x) 的解析式;
(Ⅱ)若f (x) 在 [0,1] 上是增函数,求实数a 的取值范围;
(Ⅲ)若a  Î (-6,6),问能否使f (x) 的最大值为 4?请说明理由.
Î (-6,6),问能否使f (x) 的最大值为 4?请说明理由.
(满分12分)某专卖店销售一新款服装,日销售量(单位为件)f (n) 与时间n(1≤n≤30、nÎ N*)的函数关系如下图所示,其中函数f (n) 图象中的点位于斜率为 5 和-3 的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.
(Ⅰ)求f (n) 的表达式,及前m天的销售总数;
(Ⅱ)按以往经验,当该专卖店销售某款服装的总数超过 400 件时,市面上会流行该款服装,而日销售量连续下降并低于 30 件时,该款服装将不再流行.试预测本款服装在市面上流行的天数是否会超过 10 天?请说明理由.
(满分12 分)某班有两个课外活动小组,其中第一小组有足球票6张,排球票 4张;第二小组有足球票4张,排球票6张.甲从第一小组的10张票中任抽1张,和乙从第二小组的10张票中任抽1张.
分)某班有两个课外活动小组,其中第一小组有足球票6张,排球票 4张;第二小组有足球票4张,排球票6张.甲从第一小组的10张票中任抽1张,和乙从第二小组的10张票中任抽1张.
(Ⅰ)两人都抽到足球票的概率是多少?
(Ⅱ)两人中至少有1人抽到足球票的概率是多少?
(满分12分)正方体ABCD-A1B1C1D1 的棱长为 2,且AC 与BD 交于点O,E 为棱DD1 中点,以A 为原点,建立空间直角坐标系A-xyz,如图所示.
(Ⅰ)求证:B1O⊥平面EAC;
(Ⅱ)若点  F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;
F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;
(Ⅲ)求二面角B1-EA-C 的正弦值.
(满分12分)已知△ABC中,2 tan A = 1,3 tan B = 1,且最长边的长度为 1,求角C的大小和最短边的长度.