(本小题满分12分)
如图,点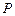 是椭圆
是椭圆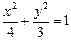 上一动点,点
上一动点,点 是点
是点 在
在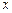 轴上的射影,坐标平面
轴上的射影,坐标平面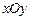 内动点
内动点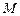 满足:
满足: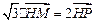 (
( 为坐标原点),设动点
为坐标原点),设动点 的轨迹为曲线
的轨迹为曲线 .
.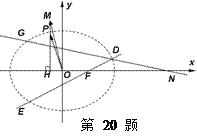
(Ⅰ)求曲线 的方程并画出草图;
的方程并画出草图;
(Ⅱ)过右焦点 的直线
的直线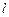 交曲线
交曲线 于
于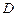 ,
, 两点,且
两点,且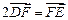 ,点
,点 关于
关于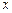 轴的对称点为
轴的对称点为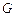 ,求直线
,求直线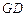 的方程.
的方程.
(本小题满分14分)
如图,在直三棱柱ABC—A1B1C1中,∠ ABC=90°,BC=2,AB=4,CC1=4,E在BB1上,且EB1=1,D、F分别为CC1、A1C1的中点。
ABC=90°,BC=2,AB=4,CC1=4,E在BB1上,且EB1=1,D、F分别为CC1、A1C1的中点。
(1)求证:B1D⊥平面ABD;
(2)求异面直线BD与EF所成的角;
(3)求点F到平面ABD的距离。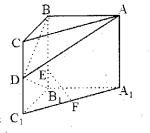
已知数列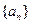 的前
的前
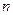 项和为
项和为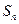 ,且
,且
(1)求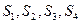 的值;
的值;
(2)猜想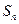 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。
(本小题满分12分)
某公司在“2010年上海世博会知识宣传”活动中进行抽奖活动,抽奖规则是:在一个盒子中装有8张大小相同的精美卡片,其中2张印有“世博会欢迎您”字样,2张印有“世博会会徽”图案,4张印有“海宝”(世博会吉祥物)图案,现从盒子里无放回的摸取卡片,找出印有“海宝”图案的卡片表示中奖且停止摸卡。
(Ⅰ)求最多摸两次中奖的概率;
(Ⅱ)用 表示摸卡的次数,求
表示摸卡的次数,求 的分布列和数学期望。
的分布列和数学期望。
(本小题满分12分)
已知 是奇函数,且在定义域(—1,1)内可导并满足
是奇函数,且在定义域(—1,1)内可导并满足 解关于m的不等式
解关于m的不等式
(本小题满分12分)
已知合集 的定义域为M,
的定义域为M, ,若
,若