如图,实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成,圆P和圆Q的
半径都是2km,点P在圆Q上,现要在公园内建一块顶点都在圆P上的多边形活动场地.
(1)如图甲,要建的活动场地为△RST,求场地的最大面积; (2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积.
(2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积.
若由数列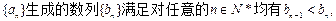
 “Z数列”
“Z数列”
(1)在数列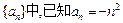 ,试判断数列
,试判断数列 是否为“Z数列”;
是否为“Z数列”;
(2)若数列 是“Z数列”,
是“Z数列”, ;
;
(3)若数列 是“Z数列”,设
是“Z数列”,设 。
。
已知抛物线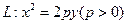 和点M(2,2),若抛物线L上存在不同的两点A、B满足
和点M(2,2),若抛物线L上存在不同的两点A、B满足 。
。
(1)求实数p的取值范围;
(2)当 时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。
时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。
已知函数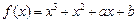
(1)当a=-1时,求函数f(x)的单调区间;
(2)若函数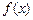 的图象与直线y=ax只有一个公共点,求实数b的取值范围。
的图象与直线y=ax只有一个公共点,求实数b的取值范围。
如图,FD垂直于矩形ABCD所在平面,CE//DF, ∠DEF=900。
(1)求证:BE//平面ADF; (2)若矩形ABCD的一个边AB="3," 另一边BC=2
(2)若矩形ABCD的一个边AB="3," 另一边BC=2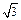 ,EF=2
,EF=2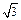 ,求几何体ABCDEF的体积。
,求几何体ABCDEF的体积。
某园林局对1000株树木的生长情况进行调查,其中槐树600株,银杏树400株. 现用分层抽样方法从这1000株树木中随机抽取100株,其中银杏树树干周长(单位:cm)的抽查结果如下表:
| 树干周长(单位:cm) |
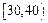 |
 |
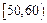 |
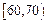 |
| 株数 |
4 |
18 |
 |
6 |
(I)求 的值 ;
的值 ;
(II)若已知树干周长在30cm至40cm之间的4株银杏树中有1株患有虫害,现要对这4株树逐一进行排查直至找出患虫害的树木为止.求排查的树木恰好为2株的概率.