本小题满分14分)
三次函数 的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.
的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.
(1)若函数f(x)为奇函数且过点(1,-3),当x<0时求 的最大值 ;
的最大值 ;
(2)若函数在x=1处取得极值-2,试用c表示a和b,并求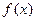 的单调递减区间;
的单调递减区间;
(3)设点A、B、C、D的横坐标分别为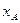 ,
,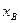 ,
, ,
,
求证 ;
;
集合A是由具备下列性质的函数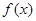 组成的:
组成的:
(1)函数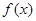 的定义域是
的定义域是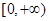 ;(2)函数
;(2)函数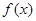 的值域是
的值域是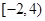 ;
;
(3)函数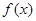 在
在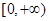 上是增函数.试分别探究下列两小题:
上是增函数.试分别探究下列两小题:
(1)判断函数 ,及
,及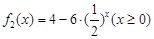 是否属于集合A?并证明.
是否属于集合A?并证明.
(2)对于(1)中你认为属于集合A的函数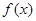 ,不等式
,不等式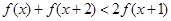 是否对于任意的
是否对于任意的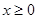 总成立?若不成立,为什么?若成立,请证明你的结论.
总成立?若不成立,为什么?若成立,请证明你的结论.
为了缓解交通压力,某省在两个城市之间特修一条专用铁路,用一列火车作为公共交通车。已知每日来回趟数 是每次拖挂车厢节数
是每次拖挂车厢节数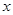 的一次函数,如果该列火车每次拖
的一次函数,如果该列火车每次拖 节车厢,每日能来回
节车厢,每日能来回 趟;如果每次拖
趟;如果每次拖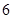 节车厢,则每日能来回
节车厢,则每日能来回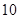 趟,火车每日每次拖挂车厢的节数是相同的,每节车厢满载时能载客
趟,火车每日每次拖挂车厢的节数是相同的,每节车厢满载时能载客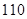 人。
人。
(1)求出 关于
关于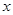 的函数;
的函数;
(2)该火车满载时每次拖挂多少节车厢才能使每日营运人数最多?并求出每天最多的营运人数?
已知函数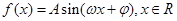 (其中A>0, ω>0,0<
(其中A>0, ω>0,0< <
< )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个最低点为
,且图象上一个最低点为 .
.
(1)求f(x)的解析式;
(2)当 ,求f(x)的值域.
,求f(x)的值域.
已知函数
(1)求函数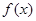 的最大值和最小值以及取最大、最小值时相应
的最大值和最小值以及取最大、最小值时相应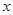 的取值集合;
的取值集合;
(2)写出函数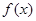 的单调递增区间.
的单调递增区间.
(3)作出此函数在一个周期内的图像。
已知函数 且
且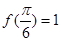
(1)求 的最小值及此时函数
的最小值及此时函数 的表达式
的表达式
(2)将(1)中所得函数 的图像结果怎样变换可得
的图像结果怎样变换可得 的图像
的图像