为了缓解交通压力,某省在两个城市之间特修一条专用铁路,用一列火车作为公共交通车。已知每日来回趟数 是每次拖挂车厢节数
是每次拖挂车厢节数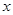 的一次函数,如果该列火车每次拖
的一次函数,如果该列火车每次拖 节车厢,每日能来回
节车厢,每日能来回 趟;如果每次拖
趟;如果每次拖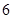 节车厢,则每日能来回
节车厢,则每日能来回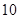 趟,火车每日每次拖挂车厢的节数是相同的,每节车厢满载时能载客
趟,火车每日每次拖挂车厢的节数是相同的,每节车厢满载时能载客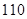 人。
人。
(1)求出 关于
关于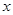 的函数;
的函数;
(2)该火车满载时每次拖挂多少节车厢才能使每日营运人数最多?并求出每天最多的营运人数?
设等差数列{an}的前n项和为Sn,已知a3=12,S12>0,S13<0.
(1)求公差d的取值范围;
(2)指出S1、S2、…、S12中哪一个值最大,并说明理由.
已知函数f(x)在(-∞,0)∪(0,+∞)上有定义,且在(0,+∞)上是增函数,f(1)=0,又g(θ)=sin2θ-mcosθ-2m,θ∈[0, ],设M={m|g(θ)<0,m∈R},N={m|f[g(θ)]<0},求M∩N.
],设M={m|g(θ)<0,m∈R},N={m|f[g(θ)]<0},求M∩N.
某工厂拟建一座平面图(如下图)为矩形且面积为200平方米的三级污水处理池,由于地形限制,长、宽都不能超过16米,如果池外周壁建造单价为每米400元,中间两条隔墙建造单价为每米248元,池底建造单价为每平方米80元(池壁厚度忽略不计,且池无盖).
(1)写出总造价y(元)与污水处理池长x(米)的函数关系式,并指出其定义域.
(2)求污水处理池的长和宽各为多少时,污水处理池的总造价最低?并求最低总造价. 
定义在(-1,1)上的函数f(x)满足①对任意x、y∈(-1,1),都有f(x)+f(y)=f(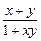 );②当x∈(-1,0)时,有f(x)>0.
);②当x∈(-1,0)时,有f(x)>0.
求证: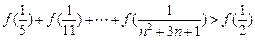 .
.
设f(x)=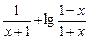 .
.
(1)证明:f(x)在其定义域上的单调性;
(2)证明: 方程f-1(x)=0有惟一解;
(3)解不等式f[x(x-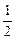 )]<
)]<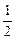 .
.