已知命题p:x∈A={x|a-1<x<a+1,x∈R},命题q:x∈B={x|x2-4x+3≥0}.
(1)或A∩B=∅,A∪B=R,求实数a,
(2)若綈q是p的必要条件,求实数a.
已知向量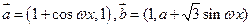 (
(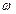 为常数且
为常数且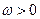 ),函数
),函数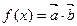 在
在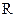 上的最大值为
上的最大值为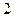 .(Ⅰ)求实数
.(Ⅰ)求实数 的值;(Ⅱ)把函数
的值;(Ⅱ)把函数 的图象向右平移
的图象向右平移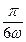 个单位,可得函数
个单位,可得函数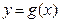 的图象,若
的图象,若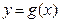 在
在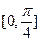 上为增函数,求
上为增函数,求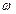 的最大值.
的最大值.
设数列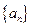 的前
的前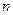 项和为
项和为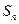 ,点
,点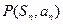 在直线
在直线 上,
上, 为常数,
为常数,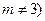 .
.
(Ⅰ)求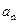 ;
;
(Ⅱ)若数列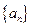 的公比
的公比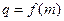 ,数列
,数列 满足
满足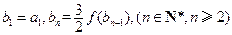 ,求证:
,求证: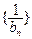 为等差数列,并求
为等差数列,并求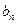 ;
;
(III)设数列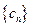 满足
满足 ,
, 为数列
为数列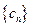 的前
的前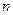 项和,且存在实数
项和,且存在实数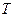 满足
满足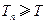 ,
,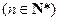 ,求
,求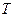 的最大值.
的最大值.
已知椭圆的方程为 ,它的一个焦点与抛物线
,它的一个焦点与抛物线 的焦点重合,离心率
的焦点重合,离心率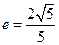 ,过椭圆的右焦点
,过椭圆的右焦点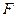 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线 ,交椭圆于
,交椭圆于 、
、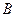 两点.
两点.
(Ⅰ)求椭圆的标准方程; (Ⅱ)设点 ,且
,且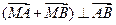 ,求直线
,求直线 的方程;
的方程;
如图,在矩形ABCD中,AB=2,BC=a,又PA⊥平面ABCD,PA=4.
(Ⅰ)若在边BC上存在一点Q,使PQ⊥QD,求a的取值范围;
(Ⅱ)当边BC上存在唯一点Q,使PQ⊥QD时,求二面角A-PD-Q的余弦值.
已知函数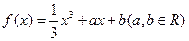 在
在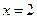 处取得的极小值是
处取得的极小值是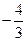 .
.
(1)求 的单调递增区间;
的单调递增区间;
(2)若 时,有
时,有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.