在一个特定的时间段内,以点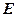 为中心的
为中心的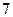 海里以内的海域被设为警戒水域,点
海里以内的海域被设为警戒水域,点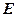 正北55海里处有一雷达观测站
正北55海里处有一雷达观测站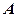 ,某时刻测得一艘匀速直线行驶的船只位于点
,某时刻测得一艘匀速直线行驶的船只位于点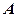 北偏东
北偏东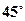 且与点
且与点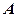 相距
相距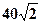 海里的位置
海里的位置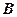 ,经过40分钟又测得该船已经驶到点
,经过40分钟又测得该船已经驶到点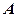 北偏东
北偏东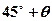 (其中
(其中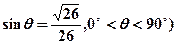 且与点
且与点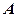 相距
相距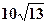 海里的
海里的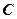 处.
处.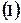 求该船的行驶速度;
求该船的行驶速度; 若该船不改变航行
若该船不改变航行 方向继续行驶,判断它是否会进入警戒线水域,并说明理由.
方向继续行驶,判断它是否会进入警戒线水域,并说明理由.
(本题14分)设抛物线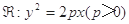 过点
过点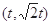 (
(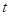 是大于零的常数).
是大于零的常数).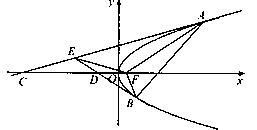
(1)求抛物线 的方程;
的方程;
(2)若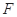 是抛物线
是抛物线 的焦点,斜率为1的直线交抛物线
的焦点,斜率为1的直线交抛物线 A,B两点,
A,B两点, 轴负半轴上的点
轴负半轴上的点 满足
满足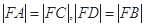 ,直线
,直线 相交于点
相交于点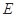 , 当
, 当 时,求直线
时,求直线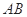 的方程.
的方程.
(本题14分)如图所示,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan∠BCO=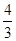 .
.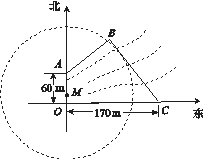
(1)求新桥BC的长.
(2)当OM多长时,圆形保护区的面积最大?
(本题13分)已知椭圆C:x2+2y2=4.
(1)求椭圆C的离心率;
(2)设O为原点,若点A在直线y=2上,点B在椭圆C上,且OA⊥OB,求线段AB长度的最小值.
(本题12分)已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为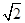 ,且过点(4,-
,且过点(4,-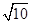 ).
).
(1)求双曲线方程;
(2)若点M(3,m)在双曲线上,求证:点M在以F1F2为直径的圆上;
(3)在(2)的条件下求△F1MF2的面积.
(本题12分)已知命题p:方程2x2+ax-a2=0在[-1,1]上有解;命题q:只有一个实数x0满足不等式x02+2ax0+2a≤0,若命题“p或q”是假命题,求a的取值范围.