已知函数f(x)＝为奇函数，f(1)＜f(3)，
且不等式0≤f(x)≤的解集是{x|－2≤x≤－1或2≤x≤4}．
(1)求a，b，c的值；
(2)是否存在实数m使不等式f(－2＋sinθ)＜－m2＋对一切θ∈R成立？若存在，求出m的取值范围；若不存在，请说明理由．
数列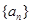
的前
项和是
，且
．
（1）求数列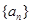的通项公式；
（2）记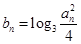
，数列
的前项和为
，证明：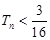
．
（本小题满分12分）已知函数
.
（1）求函数
在
处的切线方程；
（2）若
在
上为单调函数，求实数
的取值范围；
（3）若在
上至少存在一个
，使得
成立，求实数
的取值范围.
（本小题满分12分）如图，已知点
是离心率为
的椭圆
：
上的一点，斜率为
的直线
交椭圆于
、
两点，且
、、三点互不重合．
（1）求椭圆的方程；
（2）求证：直线
，
的斜率之和为定值．
（本小题满分12分）已知函数 
（1）求曲线 
在点 
处的切线方程；
（2）证明：当
时， 
．
（本小题满分12分）如图, 四棱柱
的底面
是正方形,
为底面中心, 
平面.
（1）证明: 
平面
；
（2）求三棱柱
的体积.