如图，四棱锥S－ABCD的所有棱长均为1米，一只小虫从S点出-优题课

如图，四棱锥S－ABCD的所有棱长均为1米，一只小虫从S点出发沿四棱锥爬行，若在每顶点处选择不同的棱都是等可能的．设小虫爬行n米后恰回到S点的概率为P_n(n≥2，n∈N)．
(1)求P₂，P₃的值；
(2)求证：3P_n_＋₁＋P_n＝1(n≥2，n∈N)；
(3)求证：P₂＋P₃＋…＋P_n＞(n≥2，n∈N)．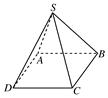

科目数学题型解答题难度较易

如图，椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ 的顶点为 $A_{1}, A_{2}, B_{1}, B_{2}$ ，焦点为 $F_{1}, F_{2}$ ， $|A_{1} B_{1}| = \sqrt{7}, S_{B_{1} A_{1} B_{2} A_{2}} = 2 S_{B_{1} F_{1} B_{2} F_{2}}$ .

（Ⅰ）求椭圆 $C$ 的方程；
(Ⅱ)设 $n$ 为过原点的直线， $l$ 是与 $n$ 垂直相交于 $P$ 点，与椭圆相交于 $A, B$ 两点的直线， $|\overset{⇀}{O P}| = 1$ .是否存在上述直线 $l$ 使 $\overset{⇀}{O A} \cdot \overset{⇀}{O B} = 0$ 成立？若存在，求出直线 $l$ 的方程；并说出；若不存在，请说明理由.

为了解学生身高情况，某校以 $10 %$ 的比例对全校 $700$ 名学生按性别进行分层抽样检查，测得身高情况的统计图如下：

（Ⅰ）估计该校男生的人数；
（Ⅱ）估计该校学生身高在 $170 ~ 185 c m$ 之间的概率；
（Ⅲ）从样本中身高在 $180 ~ 190 c m$ 之间的男生中任选 $2$ 人，求至少有 $1$ 人身高在 $185 ~ 190 c m$ 之间的概率.

如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是矩形， $P A ⊥$ 平面 $A B C D$ ， $A P = A B$ ， $B P = B C = 2$ ， $E, F$ 分别是 $P B, P C$ 的中点.
(Ⅰ)证明： $E F / /$ 平面 $P A D$ ；
(Ⅱ)求三棱锥 $E - A B C$ 的体积 $V$ .

在 $△ A B C$ 中，已知 $B = 45^{°}$ , $D$ 是 $B C$ 边上的一点， $A D = 10, A C = 14, D C = 6$ ，求 $A B$ 的长.

已知 ${a_{n}}$ 是公差不为零的等差数列， $a_{1} = 1$ ，且 $a_{1}, a_{3}, a_{9}$ 成等比数列.
（Ⅰ）求数列 ${a_{n}}$ 的通项;

（Ⅱ）求数列 ${2^{a_{n}}}$ 的前 $n$ 项和 $S_{n}$ .

试卷网试题网古诗词网作文网范文网