如图,在四棱锥
中,底面
是矩形,
平面
,
,
,
分别是
的中点.
(Ⅰ)证明:
平面
;
(Ⅱ)求三棱锥
的体积
.

已知函数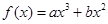 ,当
,当 时,有极大值
时,有极大值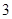 .
.
(1)求 的值;
的值;
(2)求函数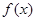 的极小值.
的极小值.
给定数列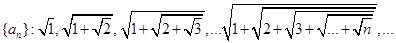
(1)判断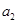 是否为有理数,证明你的结论;
是否为有理数,证明你的结论;
(2)是否存在常数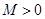 .使
.使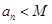 对
对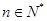 都成立? 若存在,找出
都成立? 若存在,找出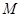 的一个值, 并加以证明; 若不存在,说明理由.
的一个值, 并加以证明; 若不存在,说明理由.
已知抛物线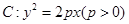 的焦点
的焦点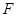 到准线的距离为
到准线的距离为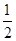 .过点
.过点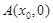
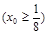
作直线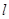 交抛物线
交抛物线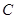 与
与 两点(
两点(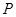 在第一象限内).
在第一象限内).
(1)若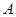 与焦点
与焦点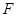 重合,且
重合,且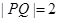 .求直线
.求直线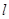 的方程;
的方程;
(2)设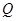 关于
关于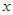 轴的对称点为
轴的对称点为 .直线
.直线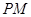 交
交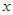 轴于
轴于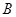 . 且
. 且 .求点
.求点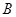 到直线
到直线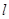 的距离的取值范围.
的距离的取值范围.
如图,四棱柱 中,
中,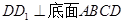 .
.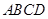 为平行四边形,
为平行四边形,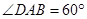 ,
, 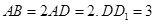 ,
, 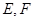 分别是
分别是 与
与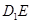 的中点.
的中点.
(1)求证: ;
;
(2)求二面角 的平面角的余弦值.
的平面角的余弦值.
某电视台“挑战60秒”活动规定上台演唱:
(I)连续达到60秒可转动转盘(转盘为八等分圆盘)一次进行抽奖,达到90秒可转两次,达到120秒可转三次(奖金累加).
(2)转盘指针落在I、II、III区依次为一等奖(500元)、二等奖(200元)、三等奖(100元),落在其它区域不奖励.
(3)演唱时间从开始到三位评委中至少1人呜啰为止,现有一演唱者演唱时间为100秒.
①求此人中一等奖的概率;
②设此人所得奖金为 ,求
,求 的分布列及数学期望
的分布列及数学期望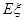 .
.