若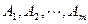
为集合
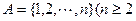且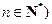
的子集，且满足两个条件：
①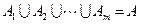
；
②对任意的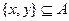
，至少存在一个
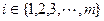，使
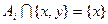或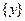
.
 |
 |
… |
 |
 |
 |
… |
 |
| … |
… |
… |
… |
 |
 |
… |
 |
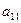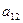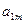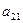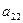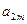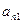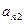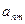则称集合组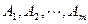具有性质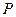
.
如图，作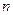
行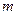
列数表，定义数表中的第
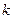行第
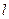列的数为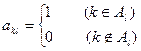
.
（Ⅰ）当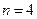
时，判断下列两个集合组是否具有性质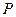，如果是请画出所对应的表格，如果不是请说明理由；
集合组1：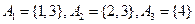
；
集合组2：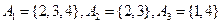
.
（Ⅱ）当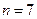
时，若集合组
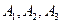具有性质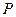，请先画出所对应的
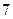行3列的一个数表，再依此表格分别写出集合；
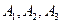（Ⅲ）当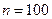
时，集合组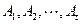
是具有性质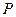且所含集合个数最小的集合组，求
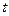的值及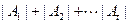
的最小值.（其中
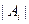表示集合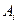
所含元素的个数）
的定义域
(a
－a
)(a>0且a
1)在(－
, +
试证明对于任意a,
为增函数
－7a
+3=0有一个根是2, 求a的值和方程其余的根