在边长为4的正方形ABCD上有一点P,沿着折线BCDA由B点(起点)向A点(终点)移动,设P点移动的路程为x,△ABP的面积为y=f(x).
(1)求△ABP的面积与P移动的路程间的函数关系式;
(2)作出函数的图象,并根据图象求y的最大值.
由下面四个图形中的点数分别给出了四个数列的前四项,将每个图形的层数增加可得到这四个数列的后继项.按图中多边形的边数依次称这些数列为“三角形数列”、“四边形数列” ,将构图边数增加到
,将构图边数增加到 可得到“
可得到“ 边形数列”,记它的第
边形数列”,记它的第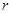 项为
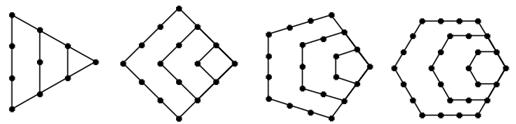
项为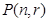 ,
,
1,3,6,10 1,4,9,16 1,5,12,22 1,6,15,28
(1)求使得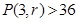 的最小
的最小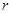 的取值;
的取值;
(2)试推导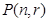 关于
关于 、
、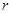 的解析式;
的解析式;
( 3)是否存在这样的“ 边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
已知函数 的图像(如图所示)过点
的图像(如图所示)过点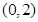 、
、 和点
和点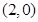 ,且函数图像关于点
,且函数图像关于点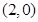 对称;直线
对称;直线 和
和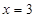 及
及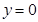 是它的渐近线.现要求根据给出的函数图像研究函数
是它的渐近线.现要求根据给出的函数图像研究函数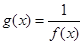 的相关性质与图像,
的相关性质与图像,
(1)写出函数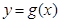 的定义域、值域及单调递增区间;
的定义域、值域及单调递增区间;
(2)作函数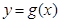 的大致图像(要充分反映由图像及条件给出的信息);
的大致图像(要充分反映由图像及条件给出的信息);
(3)试写出 的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分
的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分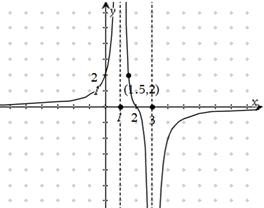
已知 为坐标原点,点
为坐标原点,点 ,对于
,对于 有向量
有向量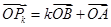 ,
,
(1)试问点 是否在同一条直线上,若是,求出该直线的方程;若不是,请说明理由;
是否在同一条直线上,若是,求出该直线的方程;若不是,请说明理由;
(2)是否在存在 使
使 在圆
在圆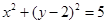 上或其内部,若存在求出
上或其内部,若存在求出 ,若不存在说明理由.
,若不存在说明理由.
一个棱长为 的正方体的八个顶角上分别截去一个三棱锥,使截掉棱锥后的多面体有六个面为正八边形,八个面为正三角形(如图所示),
的正方体的八个顶角上分别截去一个三棱锥,使截掉棱锥后的多面体有六个面为正八边形,八个面为正三角形(如图所示),
(1)求异面直线 与
与 所成角的大小;
所成角的大小;
(2)求此多面体的体积(结果用最简根式表示).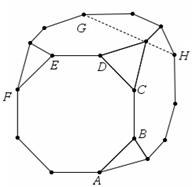
已知函数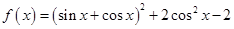 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2 )当 时,求函数
时,求函数 的最大值,最小值.
的最大值,最小值.